2 курс / Л-5.4 (2) Найпростіші задачі квантової механіки

ІV Найпростіші задачі квантової механіки

1. Рух вільної частинки

2. Частинка в нескінченно глибокій одномірній потенціальній ямі. Головне квантове число.

3. Квантовий гармонічний осцилятор.

4. Потенціальний бар’єр скінченної величини. Тунельний ефект

1. Рух вільної частинки

Найпростішим рухом квантової частинки є вільний рух. Прикладом такого руху є рух електронів в металах і напівпровідниках. В цьому випадку потенціальна енергія частинок дорівнює нулю. При вільному русі повна енергія частинки збігається з кінетичною, а її швидкість є сталою величиною. Такому рухові в класичній механіці відповідає рівномірний і прямолінійний рух.

Нехай рівномірний рух квантової частинки відбувається в напрямі осі х, яка збігається з напрямком вектора швидкості. Стаціонарне рівняння Шредінгера для вільної частинки запишеться:

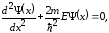(1)

де m ― маса частинки; Е ― повна енергія частинки.

Рівняння (1) є диференціальним рівнянням другого порядку зі сталими коефіцієнтами, розв’язком якого може бути функція

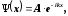(2)

де А і к ― сталі величини; і ― уявна одиниця.

Підстановка (2) в (1) дасть тотожність

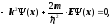
звідки

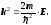(3)

У співвідношенні (3) к - хвильове число хвиль де Бройля; Е ― повна енергія частинки; m ― маса частинки.

Енергія вільної частинки з рівності (3) дорівнює

(4)

Хвильове число к може набувати довільних значень, тому що вільні частинки в системі можуть мати практично будь-які постійні швидкості. Це говорить про те, що енергетичний спектр вільних частинок є суцільним.

2.Частинка в нескінченно глибокій одномірній потенціальній ямі. Головне квантове число.

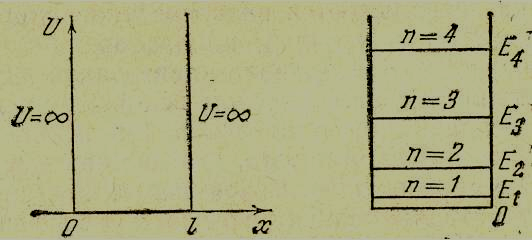
Припустимо, що частинка маси m рухається тільки вздовж вісі х. Рух частинки обмежений стінками ями в точках х=0 і х=l. Потенціальна енергія U в інтервалі 0 ≤ х ≤ l дорівнює 0, а при х < 0 і x > l дорівнює ∞. Запишемо рівняння Шредінгера для стаціонарних станів, враховуючи, що U = 0: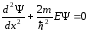

Введемо позначення: . (5)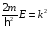

Тоді маємо рівняння, знайоме з теорії коливань:

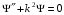
Загальним розв’язком такого диференціального рівняння являється функція, суперпозиція двох рухомих коливань:

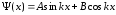
Врахуємо математичні вимоги для хвильової функції.

З умови неперервності випливає, що на границях ями Ψ повинна бути рівною нулю, тобто:

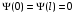
Цю умову можна задовольнити відповідним вибором величини k в рівнянні

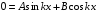
З граничної умови Ψ(0) = 0 випливає, що В = 0 , так як при sin kx = 0 cos kx ≠ 0.

Тоді з граничної умови Ψ(l)=0 маємо

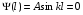
що можливо лише за умови, якщо

, (6)

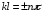
де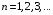

Виключивши k з рівнянь (5) і (6) знайдемо власні значення енергії частинки:

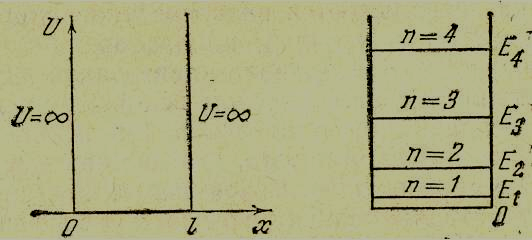Треба зазначити,що n ≠ 0 , так як при цьому Ψ ≡ 0 , що означає відсутність частинки у всьому просторі.

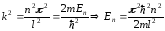
З останньої формули випливає, що існує деяка мінімальна енергія частинки, не рівна нулю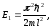

яка відповідає основному стану руху частинки. Хвильова функція цього стану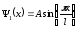

ні в якій точці всередині ями в нуль не перетворюється. Ця властивість хвильової функції основного стану має загальний характер: Хвильова функція основного стану не має вузлів, тобто не обертається в нуль всередині області, що розглядається; вона обертається в нуль лише на її кордонах.

Енергія основного стану також залежить від маси частинки та розмірів області локалізації. Зі зменшенням області локалізації енергія основного стану збільшується. Оскільки ми маємо дискретний спектр енергії частинки, то знайдемо нормуючий множник.

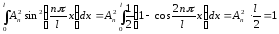
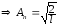
Цей множник, як бачимо, не залежить від n =1,2,3,… .

Тоді система власних функцій має вигляд:

.

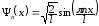
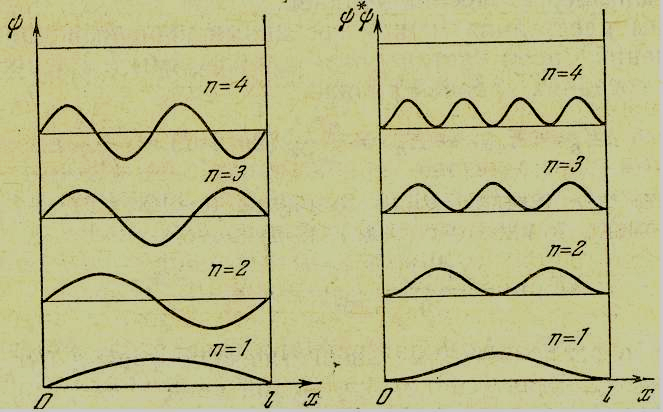
На рисунку нижче зображено хвильові функції і густина ймовірності перебування частинки в залежності від координати х. Фізичний зміст має не сама хвильова функція Ψ, а квадрат її модуля 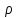= |ψ|² = ψ^* ψ

При n = 0 енергія не може бути рівною 0, так як стан з n = 0 означає, що 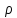= |ψ|² = ψ^* ψ = 0. В цьому випадку частинки в потенціальній ямі немає.

Висновки:

1. Енергія частинки, яка знаходиться в потенціальній ямі, - приймає дискретний ряд значень.

2. Енергія частинки не може дорівнювати нулю. Її мінімум при Е = Е₁. Це основний (нормальний) стан частинки. Всі інші стани – збуджені.

3. Дискретний характер енергетичних рівнів проявляється тим сильніше, чим менша маса частинки і менший розмір області в якій вона рухається.

4. При великих значеннях квантових чисел квантово-механічні співвідношення переходять в співвідношення класичної фізики (має місце принцип відповідності).

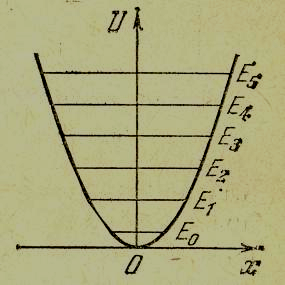
3. Квантовий гармонічний осцилятор

Гармонічним осцилятором називають частинку, яка здійснює свій рух під дією квазіпружної сили F = – kx. Потенціальна енергія такої частинки має вигляд

Тут k – коефіцієнт жорсткості.

Власна частота класичного гармонічного осцилятора , де m – маса частинки.

Тоді потенціальна енергія може бути записана так: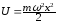

А повна енергія – зберігається.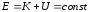

Але класична механіка – це частковий випадок більш загальної квантової механіки. І тому цікаво знати розв'язок цієї задачі з квантової точки зору.

Підставляючи U в стаціонарне рівняння Шредінгера маємо:

.

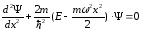
Розв’язком цього рівняння є власні функції Ψ_n(x), які мають власні значення енергії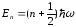

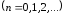
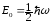
– мінімальна енергія.

Рівні енергії гармонічного осцилятора еквідистантні, тобто:

Ймовірність переходів з одного стану в інший: ∆n = ±1 .

4. Потенціальний бар’єр скінченної величини. Тунельний ефект

Класична частинка не може перебувати в тих місцях, де її потенціальна енергія U(x) перевищувала б повну енергію частинки E. Щодо квантової частинки, то вона має таку властивість через те, що існує відмінна від нуля імовірність проникнення її крізь потенціальний бар’єр, тобто в область, де U(x)  E.

Проведемо оцінку цієї імовірності шляхом розв’язування такої задачі. Нехай квантова частинка з масою m, рухаючись в напрямі осі х, вдаряється в потенціальний бар’єр кінцевої висоти U₀, тобто

причому енергія частинки Е менша висоти бар’єра U₀ .

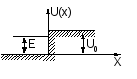
В області потенціального бар’єра рівняння Шредінгера для стаціонарних станів набуде вигляду

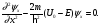(7)

Якщо позначити вира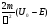з через 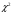, то рівняння (7) перепишеться

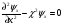. (8)

Розв’язком рівняння (8) може бути функція

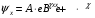, (9)

де А і В ─ деякі константи.

Експонента з додатним знаком фізичного змісту не має й може бути відкинута, тому що не повинно бути зростання імовірності перебування частинки в області потенціального бар’єра. Тому в області потенціального бар’єра (х  ), хвильова функція частинки _x визначається рівністю

_x = Аe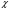^-x . (10)

Коефіцієнт А у виразі (10) пов’язаний з інтенсивністю потоку частинок, які рухаються у напрямі бар’єра, а тому задається довільно. Як правило для х   координати частинок розподіляються з густиною імовірності

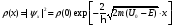, (11)

де дорівнює значенню _x² при х = 0.

Рівняння (11) показує, що із збільшенням глибини проникнення в область потенціального бар’єру, густина імовірності 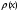зменшується експоненційно. Це зменшення буде тим швидше, чим більша різниця енергій U₀ - E.

Знайдемо глибину проникнення елементарної частинки в область потенціального бар’єра при умові, що m = 9,1 10^-31 кг (електрон), U₀ - E = 10^-4 eB, а густина імовірності 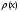на цій відстані зменшується в е разів

Ця відстань перевищує на два порядки діаметр атома водню. Глибина проникнення зменшується на порядок, якщо різниця енергій U₀ – E зросте до 10^-2 еВ.

Здатність квантових частинок проникати в область потенціального бар’єра приводить до тунельного ефекту. Його суть полягає в проникненні частинки з однієї області в іншу область, які поділені потенціальним бар’єром навіть в тих випадках, коли енергія частинки Е менша висоти потенціального бар’єра U₀.

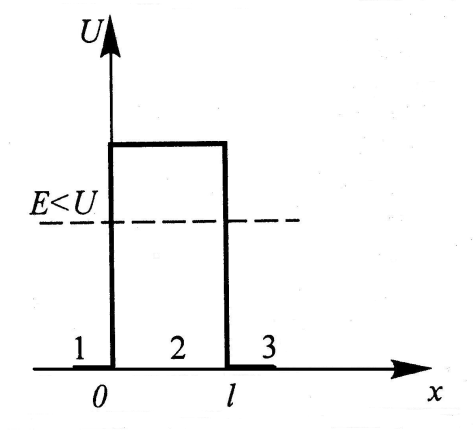
Рівняння (11) можна записати так:

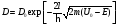, (12)

де D має смисл коефіцієнта прозорості потенціального бар’єру, l – ширина бар’єру,

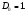
Таке проходження частинки виявляється можливим дякуючи існуванню під бар’єром хвильової функції, яка «прокладає» шлях частинці на будь-яку відстань.

Тунельний ефект є головною причиною -розпаду радіоактивних ядер.