3. Робота газу в ізопроцесах

Нехай газ, який знаходиться в циліндрі під поршнем площею S, розширюючись переміщує його на відстань dx . Тиск газу Р. За означенням елементарна механічна робота дорівнює

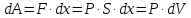, (7.6)

а загальна робота буде: 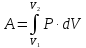. (7.7)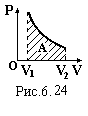

Графічно в координатах Р-V робота газу дорівнює площі криволінійної трапеції, обмеженої графіком процесу, віссю об’єму V і лініями V₁ = const, V₂ = const.

Знайдемо роботу газу в різних ізопроцесах:

1. Ізохорний. Так як V = const, dV = 0, тому dA_V = 0 і

А_V = 0. (7.8)

2) Ізобарний. Р = const. Взявши до уваги рівняння Клапейрона-Менделєєва, одержуємо

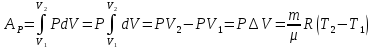. (7.9)

3) Ізотермічний. Т = const.

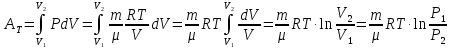. (7.10)

7.4 Молекулярно-кінетична теорія теплоємності газів

Питомою теплоємністю називається кількість теплоти, яка необхідна для нагрівання 1 кг речовини на 1К (або на 1 градус цельсія)

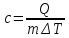[ Дж/(кг·К)] (7.11)

Молярною теплоємністю називається кількість теплоти, яка необхідна для нагрівання 1 моля речовини на 1К (або на 1 градус цельсія)

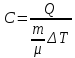[ Дж/(моль·К)] (7.12)

Ці теплоємності зв’язані між собою співвідношенням

.

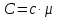Розглянемо два режими нагрівання газу: ізохорний і ізобарний.

1.Ізохорний.

При ізохорному процесі А_V = 0. Тоді, враховуючи перше начало термодинаміки (7.1) і вираз для внутрішньої енергії ідеального газу (7.5), кількість теплоти, необхідна для нагрівання 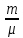молей газу на ∆Т буде .

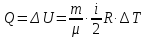Підставляємо в (7.12). Одержуємо

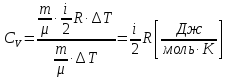. (7.13)

2. Ізобарний.

Враховуючи (7.1) і (7.9) кількість теплоти, необхідна для нагрівання 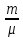молей газу на ∆Т

.

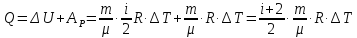Підставляємо в (7.12). Одержуємо

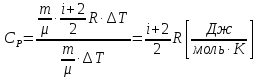. (7.14)

Рівняння (7.14) можна записати так:

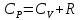. (7.15)

Його називають співвідношенням Майєра.

Теплоємність С_р > C_V тому, що при ізобарному процесі підведене тепло іде не тільки на зміну внутрішньої енергії (як при ізохорному процесі), а і на виконання роботи. Ясно, що в цьому випадку потрібно підвести більшу кількість теплоти.

Характерним для кожного газу є відношення теплоємностей

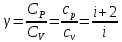. (7.16)

Одержані вирази для теплоємностей газу показують, що вони не залежать від температури. Але експеримент дає ступінчату залежність для газів багатоатомних молекул. Таку залежність неможливо пояснити в рамках класичної фізики. Вона пояснюється в рамках квантових уявлень, а саме дискретним характером зміни фізичних величин, в нашому випадку обертальної та коливальної енергії молекул. При низьких температурах теплової енергії не вистачає для збудження обертального руху молекул і коливального руху атомів в них. Тобто, обертальні і коливальні степені вільності не збуджуються. Вони послідовно починають збуджуватись при підвищенні температури. Наприклад, двохатомні молекули при зіткненні, як показано на рисунку, не приходять в обертальний рух. В той час як по класичним уявлення при такому зіткненні молекули повинні прийти в обертання. Отже, залежність С_Р (Т) зумовлена ступінчатою зміною кількості степенів вільності (числа і).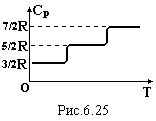