8.5. Метод Ньютона (формула «трёх восьмых»)
При
построении формулы Ньютона-Котеса
интерполирование функции
выполняется по её значениям в четырёх
точках
.
Формула «трёх
восьмых»
или формула Ньютона
будет следующей
(8.26)
Её степень точности равна трём.
Эта формула имеет следующий вид погрешности
.
Пусть
n
кратно трём
(n=3m).
Разделим отрезок
на
равных частей длины
.
Возьмём отрезок длины
:
и к нему применим формулу (8.26)
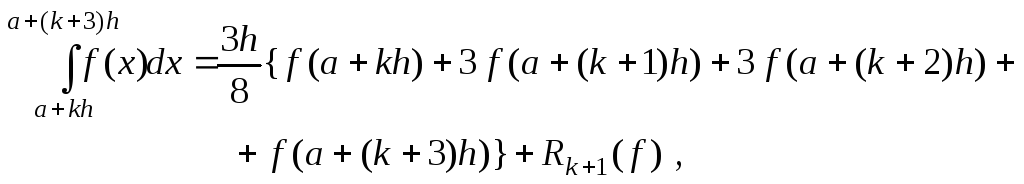
и
.
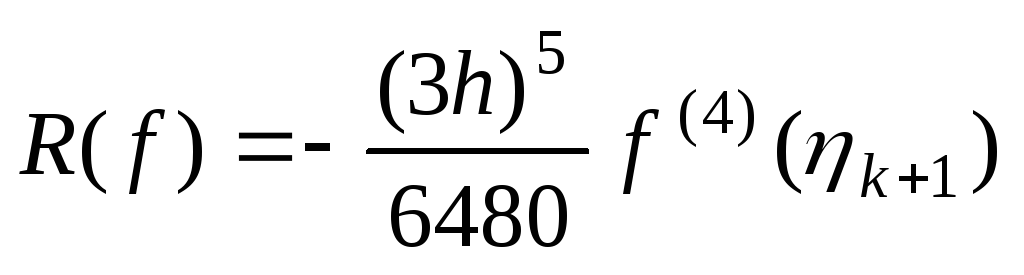Просуммировав по всем тройным отрезкам, получим следующую общую формулу «трёх восьмых»
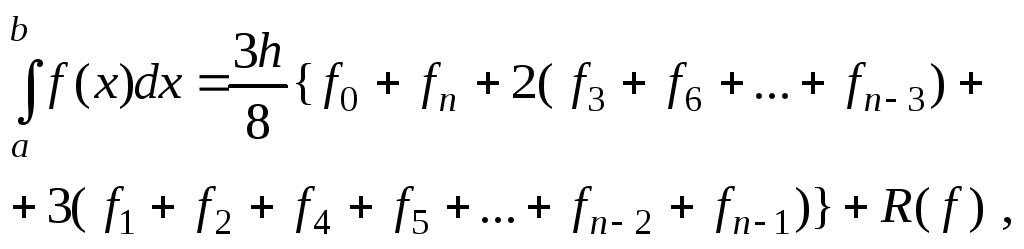
где
и погрешность
.
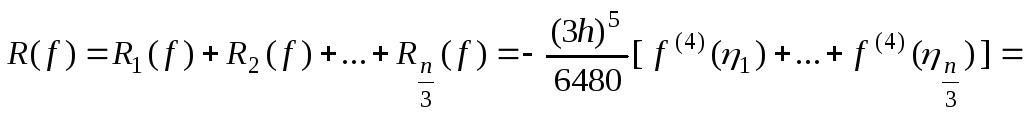
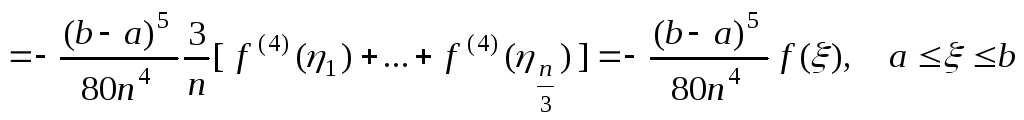В случае, когда число узлов кратно 6, лучше применять формулу Симпсона, чем формулу «трёх восьмых», так как в первом случае погрешность меньше (определяется путём сравнения).
8.6. Пример решения задачи вычисления определенного интеграла с использованием пакета Excel
Постановка
задачи. Задан
определенный интеграл
.
Определить приближенное значение интеграла методами прямоугольников, трапеций и Симпсона (парабол). Проинтегрировать аналитически и определить относительную погрешность вычислений.
Выполнение. Необходимо занести исходные данные в ячейки электронной таблицы:
|
a = |
1,5 |
|
|
b = |
2,2 |
|
|
n = |
20 |
|
|
h = |
(2,2 - 1,5) / 20 = |
0,035. |
Вычислить точное значение определенного интеграла по формуле Ньютона – Лейбница.
Точное
значение интеграла F(x)=
=
0,210529.
F(a)=0,65456866;
F(b)=0,86509805; F(b)-F(a)=0,210529.
Подготовить таблицу 8.1 с данными, необходимыми для расчета определенного интеграла различными методами.
Таблица 8.1
Расчет интеграла различными методами
|
I |
x |
y |
x+h/2 |
f(x+h/2) |
|
0 |
1,5 |
0,359211 |
1,518 |
0,355595 |
|
1 |
1,535 |
0,352046 |
1,553 |
0,348562 |
|
2 |
1,57 |
0,345142 |
1,588 |
0,341784 |
|
3 |
1,605 |
0,338486 |
1,623 |
0,335247 |
|
4 |
1,64 |
0,332067 |
1,658 |
0,328942 |
|
5 |
1,675 |
0,325872 |
1,693 |
0,322855 |
|
6 |
1,71 |
0,319891 |
1,728 |
0,316977 |
|
7 |
1,745 |
0,314113 |
1,763 |
0,311298 |
|
8 |
1,78 |
0,30853 |
1,798 |
0,305809 |
|
9 |
1,815 |
0,303132 |
1,833 |
0,300500 |
|
10 |
1,85 |
0,297911 |
1,868 |
0,295364 |
|
11 |
1,885 |
0,292858 |
1,903 |
0,290392 |
|
12 |
1,92 |
0,287966 |
1,938 |
0,285578 |
|
13 |
1,955 |
0,283227 |
1,973 |
0,280914 |
|
14 |
1,99 |
0,278636 |
2,008 |
0,276393 |
|
15 |
2,025 |
0,274185 |
2,043 |
0,272010 |
Окончание табл. 8.1
|
I |
x |
y |
х+h/2 |
F(x+h/2) |
|
16 |
2,06 |
0,269868 |
2,078 |
0,267759 |
|
17 |
2,095 |
0,265681 |
2,113 |
0,263633 |
|
18 |
2,13 |
0,261616 |
2,148 |
0,259628 |
|
19 |
2,165 |
0,25767 |
2,183 |
0,255739 |
|
20 |
2,2 |
0,253837 |
|
|
Выполнить вычисление определенного интеграла по расчетным формулам для различных методов и найти относительную погрешность каждого метода.