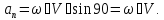1.6 Класифікація руху в залежності від значень нормального і дотичного прискорень

Так як 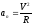, то при а_n = 0 і V ≠ 0 R → ∞. Це означає, що траєкторія являє собою пряму лінію.

При V = const. Рух рівномірний.

Розглянемо декілька варіантів значень а_n і а_τ:

1) - прямолінійний рівномірний рух;

2) 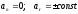- прямолінійний рівно-змінний рух;

3) - прямолінійний рух із змінним прискоренням;

4) 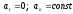- рівномірний рух з постійним радіусом кривизни траєкторії, тобто по колу;

5) - рівно-змінний рух по колу;

6) - величина швидкості зростає, так як . Отже повинен зростати і радіус кривизни траєкторії, щоб а_n залишалось незмінним. Маємо рух тіла по спіралі, яка розкручується.

1.7 Рух тіла по колу. Кутова швидкість та кутове прискорення. Аналогія поступального і обертального рухів

При вивченні обертального руху зручніше характеризувати його

не лінійними параметрами (шлях, швидкість, лінійне прискорення), а кутовим: кутом повороту, кутовою швидкістю, кутовим прискоренням. Зручність зумовлена тим, що для різних точок тіла кутові характеристики однакові на відміну від лінійних.

Дамо означення кутовим характеристикам обертального руху.

Кут повороту φ – це кут, на який повертається радіус-вектор будь-якої точки тіла. Вимірюється в радіанах. Довжина дуги (шлях S) зв’язана з кутом повороту (кутовою координатою) через радіус

.

Кутова швидкість ω - це границя відношення кута повороту ∆φ до проміжку часу ∆t, за який цей поворот здійснений, при умові, що ∆t зменшується до нуля, тобто перша похідна від кута повороту за часо .

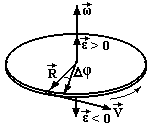
Кут повороту величина скалярна, але кутову швидкість прийнято вважати вектором, направленим вздовж осі обертання у відповідності з правилом правого гвинта: якщо обертати гвинт з правою різьбою разом з тілом, то поступальний рух гвинта вкаже напрям вектора кутової швидкості. З кінця цього вектора видно обертання тіла проти годинникової стрілки. Вимірюється кутова швидкість в рад/с, але в системі одиниць СІ рад опускається і пишеться 1/с (для узгодження з іншими розділами фізики).

Встановимо зв’язок між кутовою та лінійною швидкостями, скориставшись означеннями швидкостей.

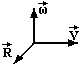
Вектори , як видно із попереднього рисунку, взаємно-перпендикулярні. Тому рівняння записують у векторній формі через векторний добуток

Кутове прискорення 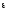- це границя відношення зміни кутової швидкості до проміжку часу ∆t, за який ця зміна відбулася, при умові, що ∆t → 0, тобто це перша похідна від кутової швидкості за часом.

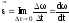
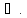
Так як вектор направлений по осі обертання, то і вектор 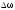, а отже і вектор кутового прискорення теж направлені вздовж осі обертання (див. рис. на попередній стор.). У випадку прискореного руху він співпадає з напрямком кутової швидкості і протилежний їй при сповільненому русі. Вимірюється кутове прискорення в 1/с².

Встановимо зв’язок між лінійним та кутовим прискореннями.

Тут

,

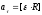відомі нам дотичне і нормальне прискорення.

Знайдемо модулі цих прискорень розкривши векторні добутки:

;
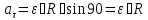