2. Дія пострілу на жорсткий лафет

До останньої чверті XIX століття у гармат ствол жорстко зв'язувався з лафетом, внаслідок чого при пострілі він не міг відкочуватися відносно лафета. Такі гармати називаються гарматами з жорстким лафетом.

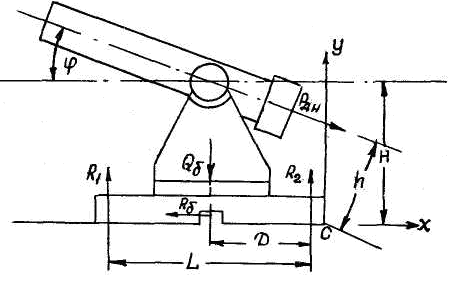
Рис. 29. Схема дії пострілу на жорсткий станок

У гармати з жорстким лафетом сила віддачі Р_дн, виникаюча в каналі ствола при пострілі, передавалася через ствол на лафет.

Внаслідок високого тиску в каналі ствола при пострілі сила Р_дн може досягати сотень тонн (100 10⁴ – 600 10⁴ Н).

Тому гармати з жорстким лафетом для забезпечення міцності і стійкості робилися важкими, при пострілі підстрибували і відкочувалися іноді на декілька метрів назад.

Гармати з жорстким лафетом не могли забезпечити:

- необхідної скорострільності;

- вони обмежували можливості тиску в каналі ствола, а отже, не могли збільшити дальність стрільби.

Для виключення впливу другорядних чинників і тих, що важко враховуються розглядаючи дію пострілу на гармату, приймаються наступні допущення:

- гармата встановлена на горизонтальній станині при КГН рівному 0 і будь-якому КВН;

- лафет і станина є абсолютно жорсткими тілами;

- всі сили, діючі на гармату, лежать у вертикальній площині симетрії;

- гармата при пострілі залишається у спокої щодо станини.

Розглянемо дію пострілу на гармату з жорстким лафетом, коли ствол жорстко зєднаний з лафетом.

Знайдемо умову, при якій лафет не буде відділятися від станини і не одержить горизонтального переміщення.

При пострілі на лафет діють наступні сили і реакції:

Р_дн – рівнодіюча сил, виникаюча при пострілі, прикладена до дна каналу ствола і направлена в протилежну сторону руху снаряда;

Q_б – сила ваги гармати, прикладена до центру коливання ствола і направлена вниз, рівна його силі тяжіння;

R₁,R₂ – вертикальна реакція основи на лафет, направлена вгору;

Rб – горизонтальна реакція бойового штиря, направлена у бік руху снаряда і прикладена до центру основи.

Щоб артсистема була нерухома і стійка під час пострілу, всі діючі сили і моменти повинні взаємно врівноважуватися, тобто сума проекцій всіх сил на осі координат і сума моментів їх щодо будь-якої точки повинні дорівнювати нулю.

Узявши проекції сил на вісь Х і моменти цих сил щодо осі, що проходять через точку С, одержимо: (1),

де D – відстань від основи до центру тяжіння системи;

L – діаметр основи станини;

 - кут стрільби;

h = Нcos - Dsin.

З першого рівняння (1) одержуємо Р_дн = R_б, тобто щоб система була нерухомою, необхідний опір штиря R_б потрібно зробити великим або таким, що дорівнює силі Рдн.

Умова нерухомості: R_б  Р_дн (2).

З другого рівняння (1) маємо:

Для стійкості системи необхідно, щоб була реакція R₁ > 0, тоді умова стійкості системи буде: , отже (3).

Розглядаючи нерівність (3), бачимо, що момент прагне обертати систему проти годинникової стрілки, а момент Р_днh - за годинниковою стрілкою, тобто прагне перекинути систему. Зробивши достатньо великою вагу системи і діаметр основи, можна досягти стійкості системи з жорсткою станиною при пострілі.