Лекции по моделированию систем / Лекция 9

Моделирование систем на основе рекуррентных уравнений.

Численные методы решения дифференциальных уравнений.

Метод Эйлера.

Рассматривается дифференциальное уравнение:

(*)

- начальные условия.

х – дискретная переменная.

Шаги:

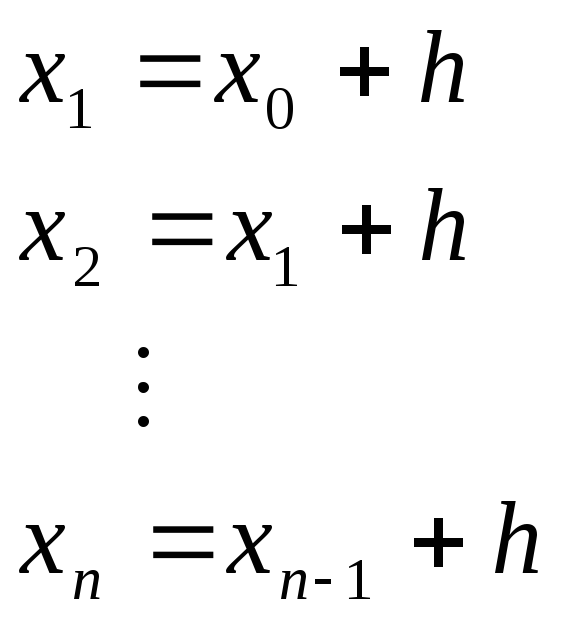
Функция может быть описана рядом Тейлора:

Далее используем:

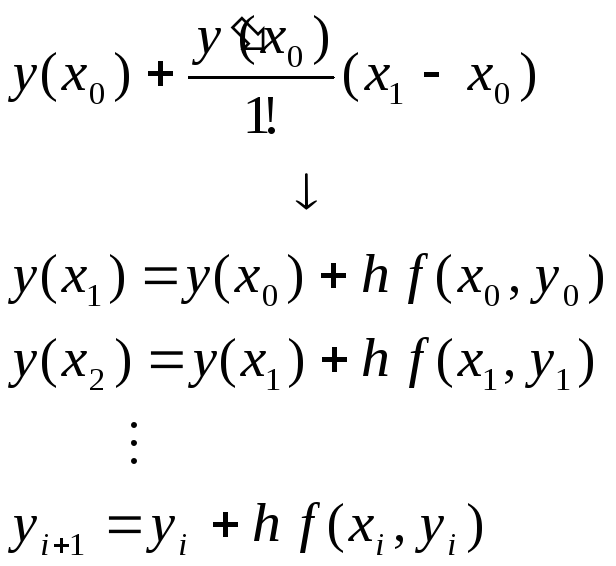
Производная равняется формуле (*).

(**)

Уравнение (**) – это рекуррентное уравнение (связывает новые значения со старыми).

- ошибка, имеет порядок .

Метод Эйлера – Коши.

Формула (**) основана на:

На новом шаге:

.

Пример: используя метод Эйлера – Коши построить модель интегратора.

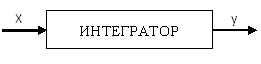
- дифференциальное уравнение.

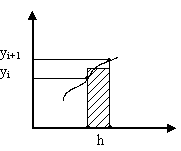
Ответ: - рекуррентное уравнение (метод прямоугольников).

Метод Рунге – Кутта (4-го порядка).

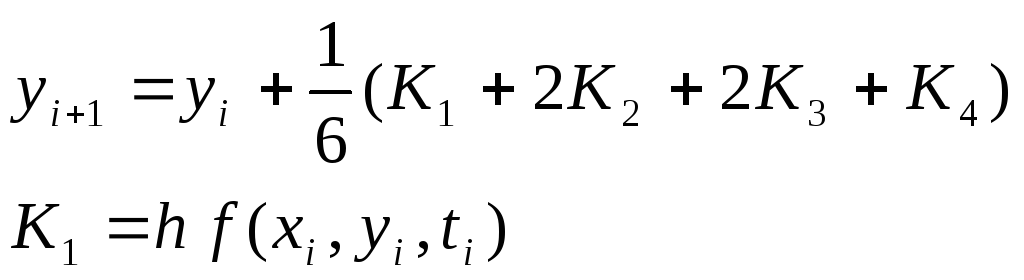
Методы дискретной аппроксимации.

Смоделировать систему:

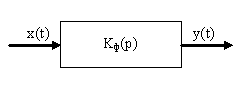
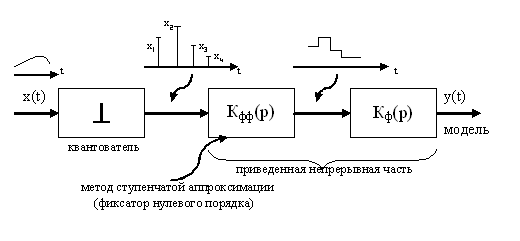
- формирующий фильтр.

Передаточная функция модели:

Z – это z - преобразование,

, где - оператор сдвига на языке z - преобразования.

,

где - оператор запаздывания.

Метод отображения.

1. Преобразование Эйлера:

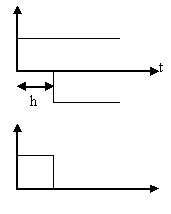
2. Метод прямоугольников:

.

3. Билинейное преобразование:

,

h – шаг по времени.

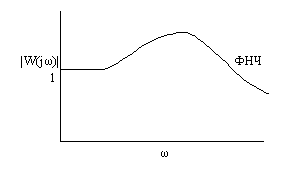
Пример:

,

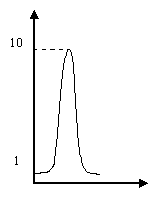
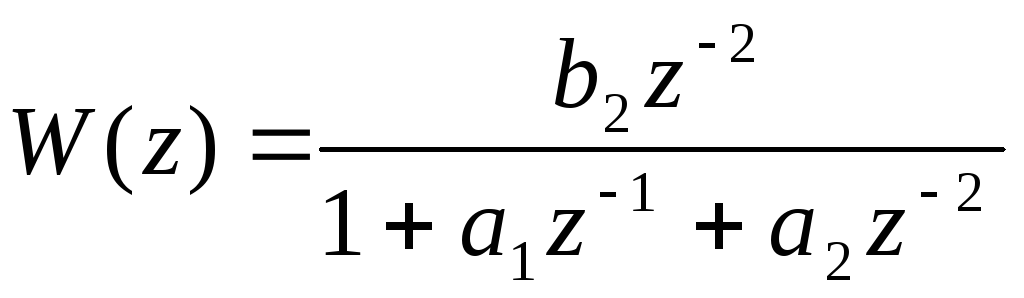- числа.

После подстановки в передаточную функцию формулу отображения надо числитель и знаменатель разделить на старшую степень z.

Задача: привести полиномы к полиномам по степени и т.д.).
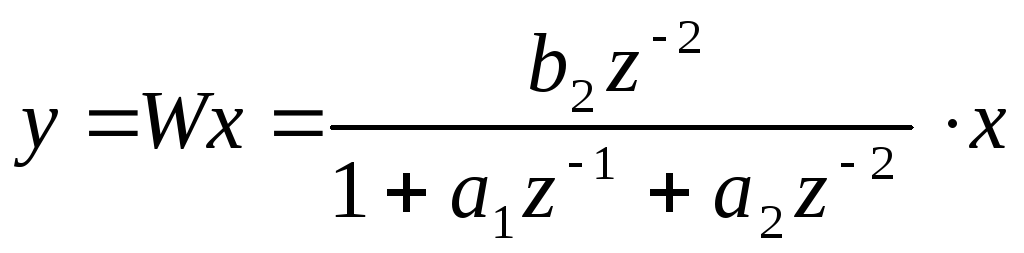