Лекции по моделированию систем / лекция 7

Если передаточная функция имеет вид , то можно записать систему в виде:

,

x - вектор состояний:

У нас , следовательно, .

Матрицы А и В связаны с передаточной функцией:

,

Пример: система описывается передаточной функцией . Дать описание модели в пространстве состояний.

У нас система 2-го порядка n = 2 (старшая степень полинома).

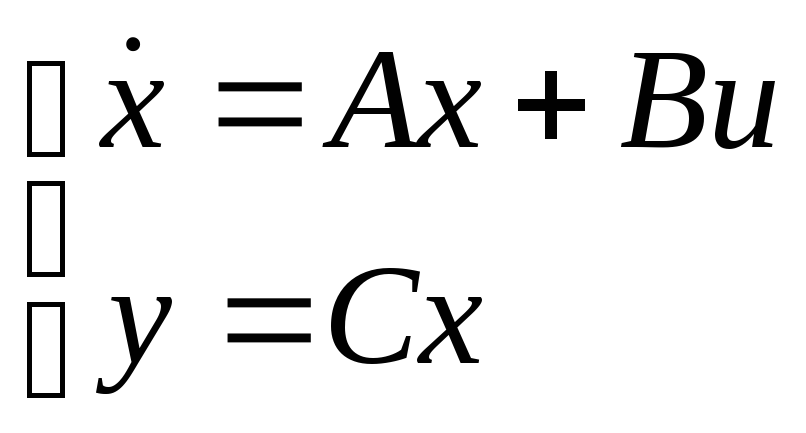
Правило умножения матриц:

От матричных уравнений переходим к скалярным (перемножаем матрицы):

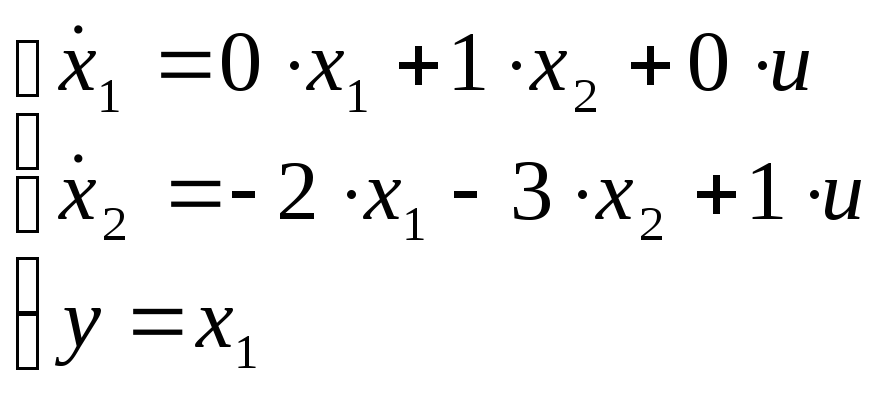
Упрощаем:

- система уравнений 1-го порядка.

Модель в пространстве состояний при передаточной функции, заданной в канонической форме.

,

λ – корни полинома.

Как найти матрицы А и В?

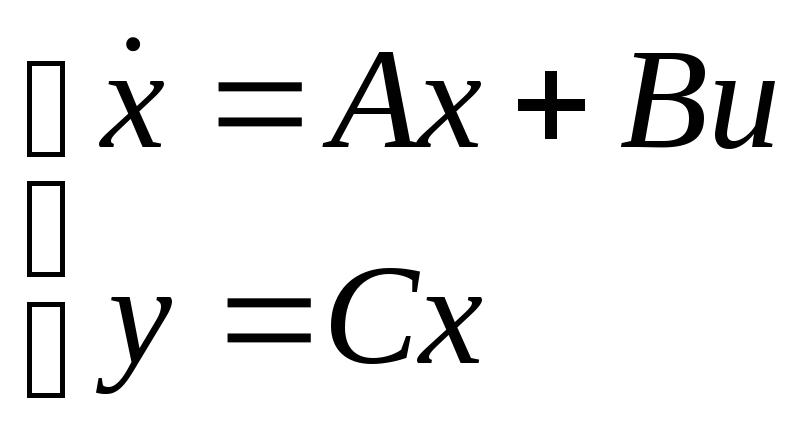
Пример:

Тогда в канонической форме:

Модель в пространстве состояний при передаточной функции, заданной в форме простых множителей.

- форма простых множителей,

- корни полинома.

Модель:

Скалярная форма:

Эта система соответствует системе: .

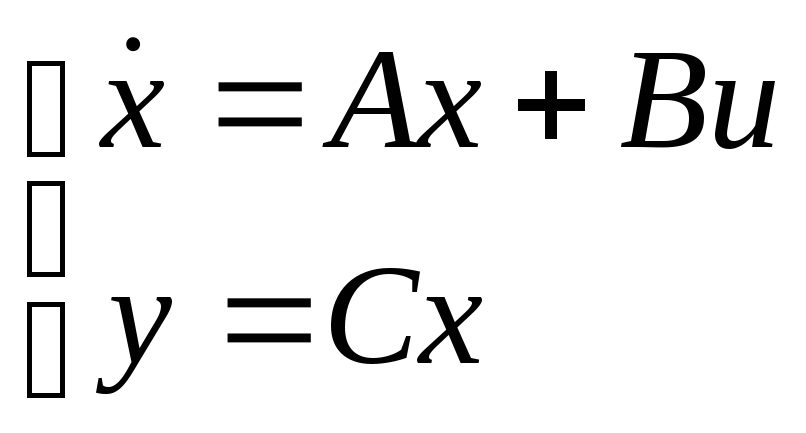Структурная схема.

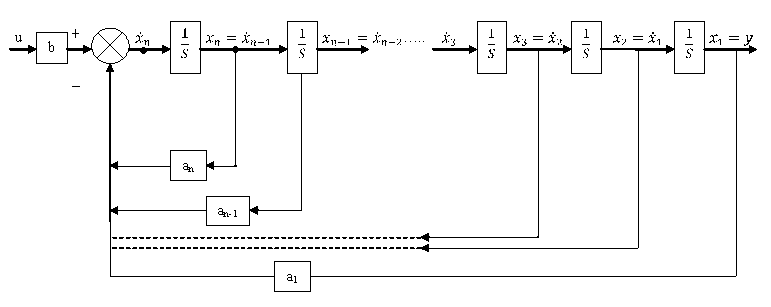
Сигналы приходят со знаком «+».

- старшая производная.

Пример: построить структурную схему модели передаточной функции .

Принцип уравнения: . Далее: .

Строим схему (находим старшую переменную и «идем» от нее):

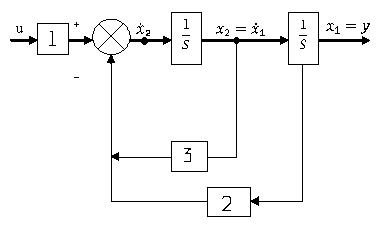
Решение дифференциальных уравнений на ЭВМ.

Моделирование в Matlab с использованием редактора решений дифференциальных уравнений (Differential Equation Editor – DEE).

В Matlab заполняем окно:

,

- окно начальных условий .

- окно желаемого результата.

Далее составляем нужную схему:

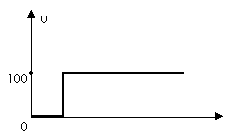
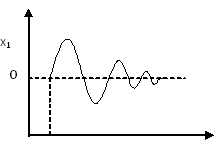
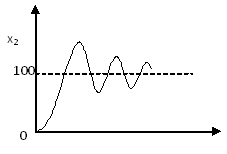
Получаем 3 графика: