Лекции по моделированию систем / лекция 8

Использование представления системы в виде схемы, полученной по дифференциальному уравнению для решения в Matlab.

Решение дифференциальных уравнений с использованием Matsab/Simulink.

Пример: 1) решить дифференциальное уравнение, описывающее систему .

,

где W(s) – передаточная функция;

P(s) и Q(s) – полиномы относительно переменных s.

Идем обратным путем:

.

При замене получается дифференциальное уравнение:

,

.

2) составляем схему, использующую блоки

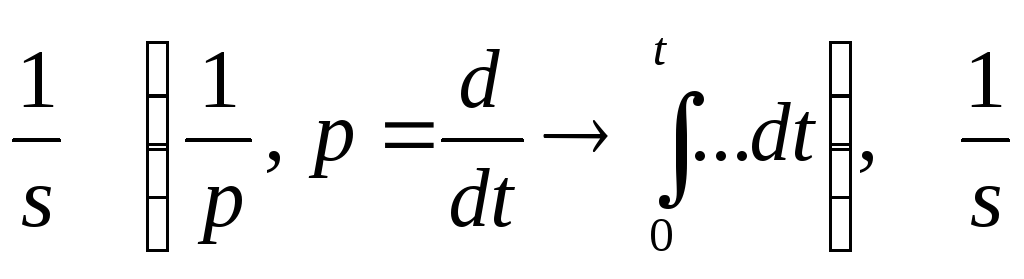- интегратор.

u – входное воздействие.

При отсутствии входного воздействия u = 0, дифференциальное уравнение имеет вид: .

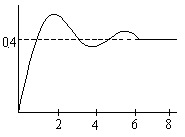
Использование библиотечных функций для решения

дифференциальных уравнений.

Решение в Matlab.

Пример: решить систему, описываемую дифференциальным уравнением . (1)

Входное воздействие u = 2.

1. Составляем функцию, описывающую правые части системы дифференциальных уравнений 1-го порядка.

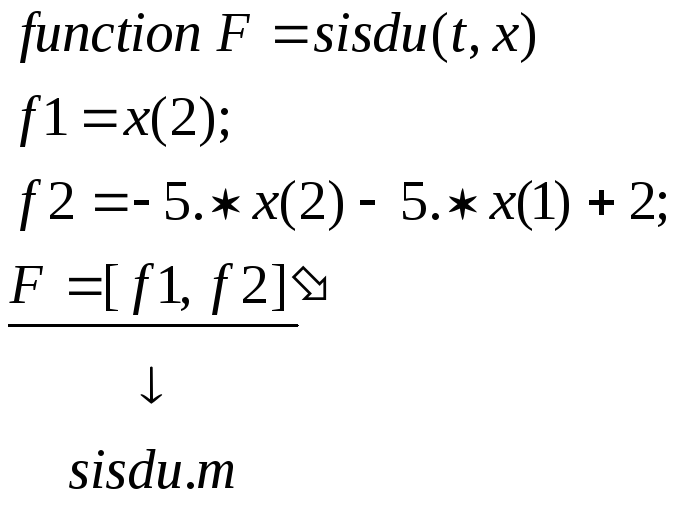
- первый вектор конструкции x;

, .

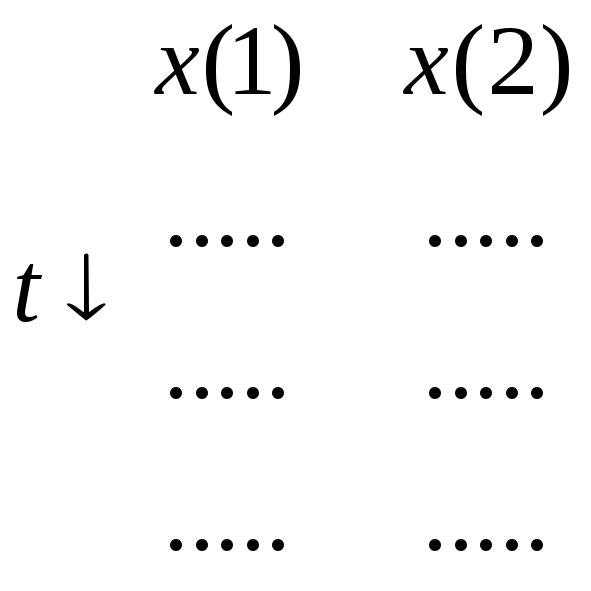
Символ .* - поэлементное перемножение.

Для библиотечной функции нужен вектор .

Команды:

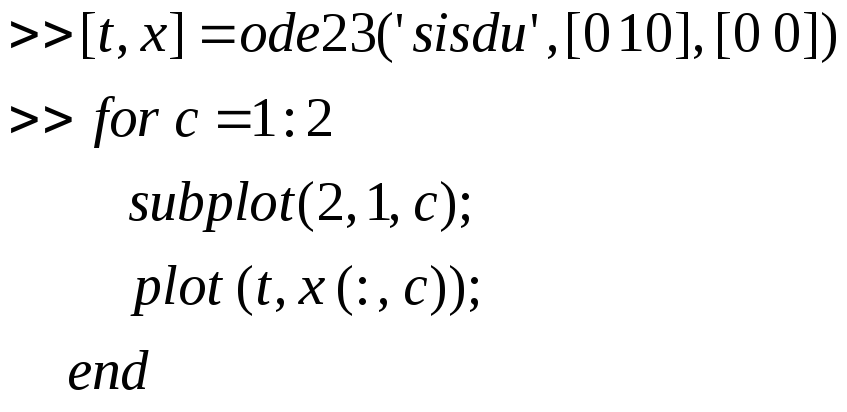
ode – обыкновенное дифференциальное уравнение;

- файл с правыми частями;

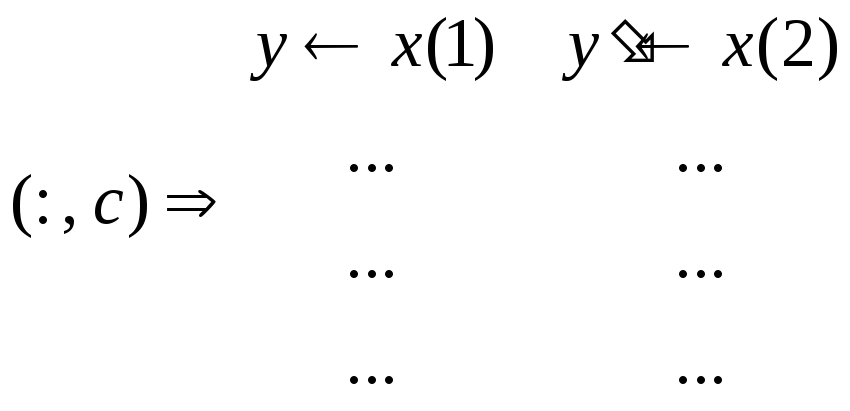
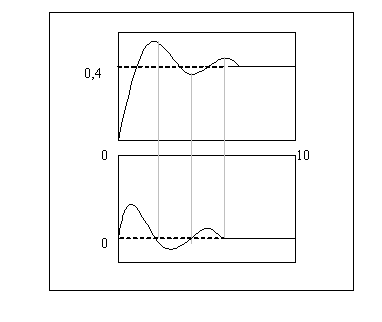
Решение в Mathcad.

Составим программу, описываемую дифференциальным уравнением . Входное воздействие u = 2.

,
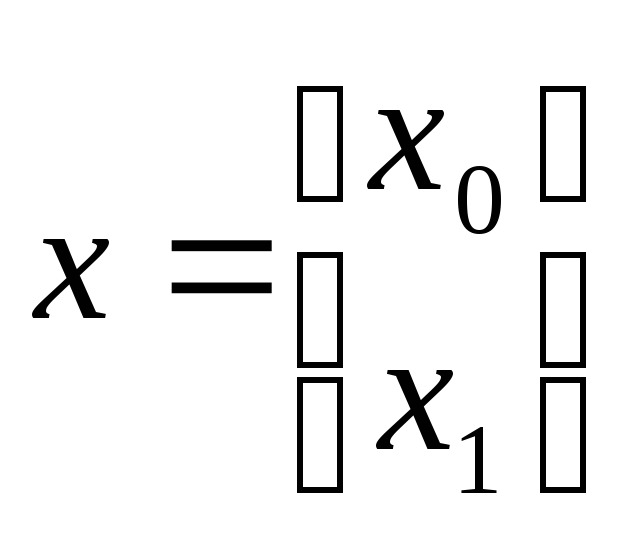