Лекции по моделированию систем / лекция 3

(1)

- неоднородное уравнение (U≠0).

-импульсная реакция.

- вход.

Если применить преобразование Лапласа к выражению (1), то получим:

(2)

- преобразование Лапласа.

(3)

Сравнивая выражение (2) и (3), получим:

= (4) = (5)

Из выражения (4) следует, что, если взять преобразование Лапласа от импульсной реакции, то получим передаточную функцию .

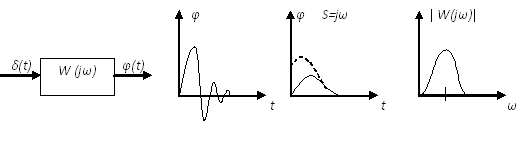
- выход.

- вход.

- передаточная функция.

- амплитудно-частотная характеристика.

φ – фаза-частотная характеристика.

Моделирование детерминированных (неслучайных) сигналов.

Явный метод.

Этот метод основан на прямом расчете сигнала по функциональным соотношениям с использованием библиотечных функций языка программирования.

1. 

signal

2. , (t → k•Δt)

k•Δt - дискретный эквивалент времени t.

Здесь используется библиотечная функция синус. Синусоида строится по точкам.

3. Комплексное представление сигналов.

ЧМ сигнал: - гармонический закон модуляции.

- девиация частоты.

- частота модуляции.

Метод комплексного представления.

Начальные данные:

, , , , ,

Теорема Котельникова: (теория)

На практике: .

- несущая в комплексном представлении.

- комплексное представление.

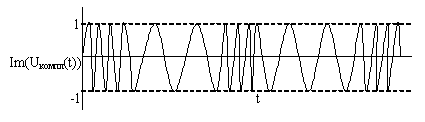
Импульсные сигналы, кодовые последовательности.

Функция Хевисайда – единичный скачок.

Ф(х)

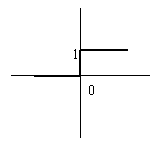
~ if(x<0,0,1)

0 – условие.

0 – тогда.

1 – противный случай.

,

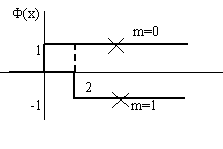
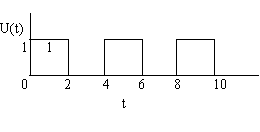
Для разности:

,

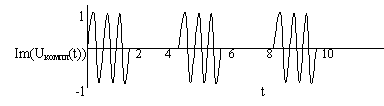
Использование циклов (программные блоки).

,

, floor – округление.

А:= j ← 0

for RGM 0.01,0.07,0.155

for i 0..

j ← j+1

Смоделировать сигнал системы посадки ILS.

RGM – разность глубин модуляции (если RGM=0, то летим правильно).