12. Поле зарядженої осі.

П

Рис. 5.2. До розрахунку електричного поля зарядженої осі.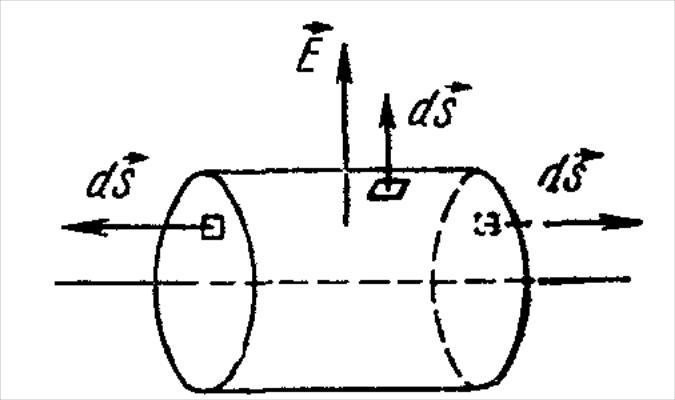

ід зарядженою віссю розуміють теоретично нескінченно довгий провідник. Заряд на одиницю довжини осі приймемо рівним τ. Для знаходження напруженості поля в точці, розташованої на відстані r від осі, проведемо через цю точку циліндричну поверхню так, щоб вісь цього циліндра збігалася із зарядженою віссю. З міркувань симетрії ясно, що напруженість поля у всіх точках циліндричної поверхні буде однаковою. Замкнена поверхня утворюється бічною поверхнею й двома денцями циліндра. На поверхні циліндра вектор, що зображує елемент поверхні циліндра ds перпендикулярний поверхні циліндра й по напрямкові завжди збігається з вектором напруженості електричного поля E. Потік вектора E через денця циліндра відсутній, тому що елемент поверхні денця перпендикулярний вектору напруженості електричного поля E.

Використовуючи теорему Гауса одержуємо:

Ми обчислюємо поверхню циліндра одиничної довжини й використовуємо заряд, що доводиться на ту ж одиницю довжини.

13. Поле двох заряджених осей.

При розгляді електричного поля у вакуумі (а також у повітрі) встановлено, що напруженість поля лінійно залежить від заряду тіла Q = const. Тому при напруженості результуючого поля від дії кількох заряджених тіл використовують принцип накладання полів.

У кожній точці простору, який оточує заряджені тіла, електричне поле одного тіла накладається на поле іншого.

Для визначення загальної напруженості треба знайти значення і напрям вектора напруженості кожної із складових полів, а потім додати вектори:

Принцип накладання дійсний і при визначенні потенціалу в деякій точці результуючого поля. Проте потенціали додають алгебраїчне, оскільки це скалярні величини:

14. Поле двопровідної лінії.

Основною хвилею двопровідної лінії передачі є Т-хвиля, для якої відсутні випромінювання і дисперсія. Хвильовий опір двопровідної лінії

, (7.15)

де r – радіус поперечного перерізу провідника, a – відстань між ними. Коефіцієнт згасання хвилі

. (7.16)

Поширення Т-хвиль у двопровідних довгих лініях можна не тільки досліджуючи зміни характеристик поля, наприклад, та (шляхом пошуку розв’язку системи рівнянь Максвелла) але й вивчаючи зміни сили струму і напруги вздовж провідників лінії. Останні задовольняють так звані телеграфні рівняння. У випадку гармонійної залежності сили струму і напруги від часу, ці рівняння набувають вигляду

, (7.17)

, (7.18)

де G, R, C та L, відповідно, – провідність між проводами лінії, опір, ємність та індуктивність лінії, розраховані на одиницю її довжини; z – координата точок лінії вздовж напрямку поширення хвилі.

Систему диференціальних рівнянь першого порядку (7.17), (7.18) можна звести до одного рівняння другого порядку, наприклад, відносно сили струму

, (7.19)

загальним розв’язком якого є суперпозиція плоских хвиль, що поширюються у протилежних напрямках вздовж лінії:

, (7.20)

де – коефіцієнт поширення хвилі.

Зв’язок сили струму з напругою між проводами лінії можна знайти з (7.20) і (7.17). Для хвилі, що поширюється в додатному напрямку осі OZ, одержується

, (7.21)

звідки імпеданс лінії

. (7.22)

Якщо в лінії відсутні втрати (G = R = 0), то , а Z_хв = , де ε і μ – діелектрична і магнітна проникності середовища, що оточує проводи лінії. За допомогою телеграфних рівнянь визначають відбиття хвиль у лінії від неоднорідних ділянок – під’єднаних до неї навантажень і т.п.

15. Ємність.

Нагадаємо, який компонент електричного кола може накопичувати електричнуенергію. Цей елемент – конденсатор. Відомо, що основним функціональним параметром конденсатора є електрична ємність. Для кожного відокремленого провідника відношення є сталою величиною і називається ємністю. Тобто ємність визначають як відношення накопиченого в конденсаторі заряду до прикладеної до нього напруги різниці потенціалів:

.

За одиницю ємності приймають ємність такого конденсатора, в якому накопичується заряд 1Кл при підключенні конденсатора до напруги 1В. Ця одиниця має назву фарад (Ф): 1Ф =1Кл/1В. Для тіл сферичної форми: , тому електрична емність провідника сферичної форми:

,

де - радіус сфери. З цієї рівності бачимо, що ємність провідників залежить від їх розмірів, форми, властивостей середовища.