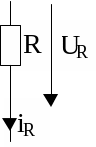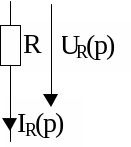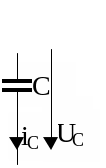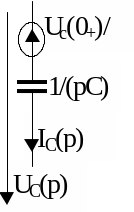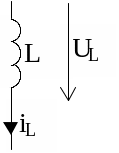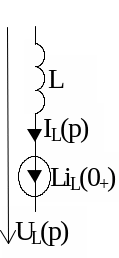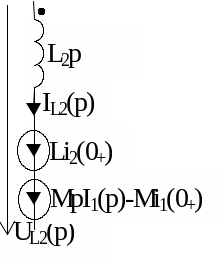19.3Акони Ома та Кірхгофа в операторній формі.

Закон Ома в операторній формі

Нехай маємо деяку вітку (див. рис. 1), виділену з деякою

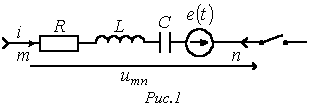
складного ланцюга. Замикання ключа у зовнішній ланцюга призводить до перехідного процесу, при цьому початкові умови для струму в гілці і напруги на конденсаторі в загальному випадку ненульові.

Для миттєвих значень змінних можна записати:

.

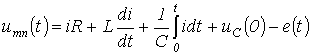Тоді на підставі наведених вище співвідношень отримаємо:

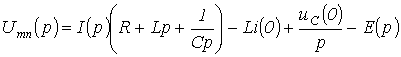
Звідси

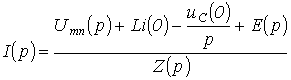, (1)

де 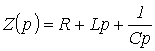- операторний опір розглянутого ділянки ланцюга.

Слід звернути увагу, що операторний опір відповідає комплексному опору ітки в ланцюзі синусоїдального струму при заміні оператора р на .

Рівняння (1) є математична запис закону Ома для ділянки кола з джерелом ЕРС в операторної формі. Відповідно до нього для гілки на рис. 1 можна намалювати операторну схему заміщення, представлену на рис. 2.

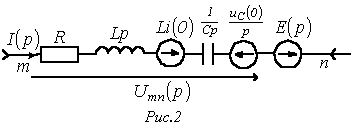
Закони Кірхгофа в операторної формі.

Перший закон Кірхгофа: алгебраїчна сума зображень струмів, що сходяться у вузлі, дорівнює нулю

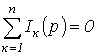
Другий закон Кірхгофа: алгебраїчна сума зображень ЕРС, що діють в контурі, дорівнює алгебраїчній сумі зображень напружень на пасивних елементах цього контуру

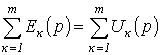
При запису рівнянь за другим законом Кірхгофа слід пам'ятати про необхідність врахування ненульових початкових умов (якщо вони мають місце). З їх урахуванням останнє співвідношення може бути переписано в розгорнутому вигляді

.

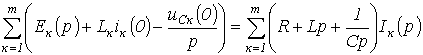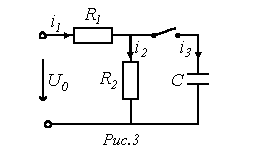
Як приклад запишемо вираз для зображень струмів в ланцюзі на рис.3 для двох випадків:

1 - ;

2 - .

У першому випадку відповідно до закону Ома

.

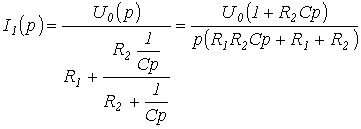Тоді

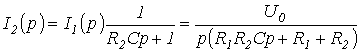
і

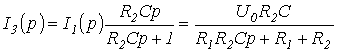
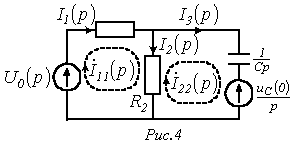
У другому випадку, тобто при , для ланцюга на рис. 3 слід скласти операторну схему заміщення, яка наведена на рис. 4. Зображення струмів в ній можуть бути визначені будь-яким методом розрахунку лінійних ланцюгів, наприклад, методом контурних струмів:

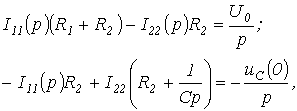
Звідки ; і .

20.Внутрішні е.Р.С. В колах з перехідним процесом.

Рівняння (1) може бути названо законом Ома в операторної формі для ділянки кола, що містить е.р.с. Воно записано при нульових початкових умовах.

Доданок Li(0) являє собою внутрішню е.р.с., обумовлену запасом енергії в магнітному полі індуктивності L вследствии протікання через неї струму i(0) безпосередньо до комутації.

Доданок u_С(0)/р являє собою внутрішню е.р.с., обумовлену запасом енергії в електричному полі конденсатора внаслідок наявності напруги на ньому uc(0) безпосередньо до комутації

Відповідно до формули (1) на рис. 2 зображена операторна схема заміщення ділянки кола рис. 1. Операторні опору R, pL, 1/(Ср). Як випливає з формули (1), внутрішня е.р.с. Li(0) спрямована згідно з напрямком струму І(р), внутрішня е.р.с. Uс(0)/p - зустрічно току І(р).

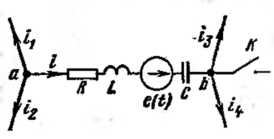
Рис.1

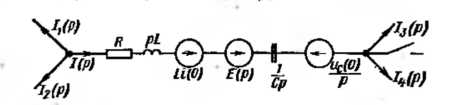
Рис.2

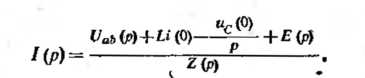
(1)

21.Операторна схема заміщення кола.

Операторні схеми заміщення елементів ланцюгів отримують на основі властивостей перетворення Лапласа.

Властивості перетворення Лапласа:

1. Лінійність:

.

2. Теорема інтегрування:

3. Теорема диференціювання:

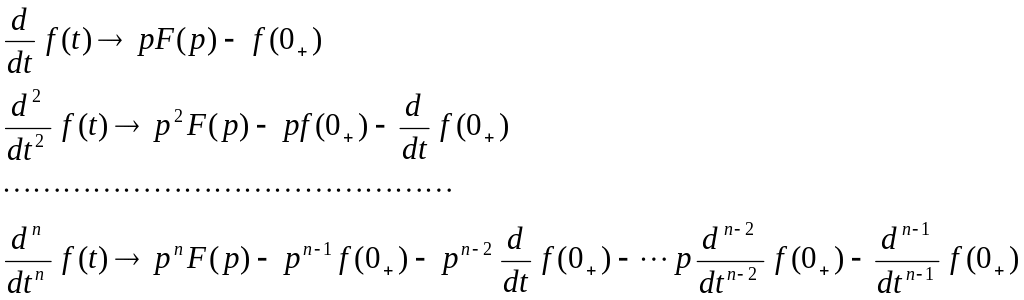
4. Теорема запізнювання:

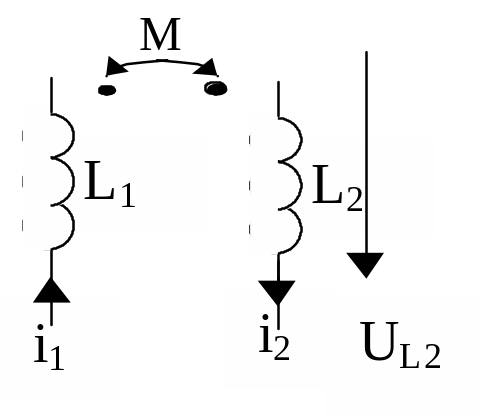
Операторні схеми заміщення елементів кола.

ОРИГІНАЛ				ЗОБРАЖЕННЯ