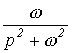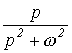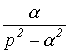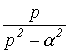- •1.Чотириполюсник і його властивості.
- •2.Рівняння в а-формі.
- •3.Методи визначення коефіцієнтів чотириполюсника.
- •4.Схеми заміщення чотириполюсників.
- •5.Зв’язок параметрів схеми заміщення з коефіцієнтами чотириполюсника.
- •6.Представлення несинусоїдного струму чи напруги у вигляді ряду Фур'є.
- •7.Вплив симетрії форми кривих несинусинусоїдного струму (напруги) на значення коефіцієнтів розкладу в ряд Фур'є.
- •8. Алгоритм розрахунку лінійних електричних кіл при дії джерел несинусоїдних струмів чи напруг.
- •9.Параметри і коефіцієнти, що характеризують несинусоїдні струми і напруги.
- •10. Потужність в лінійних колах з несинусоїдними струмами та напругами.
- •11.Перехідні процеси в електричному колі.
- •12.Причини виникнення перехідних процесів. Методи розрахунку.
- •13.Методи одержання характеристичного рівняння перехідного процесу.
- •14.Закони комутації і їх обґрунтування.
- •15.Класичний метод розрахунку перехідних процесів.
- •16.Знаходження сталих інтегрування в класичному методі розрахунку перехідних процесів.
- •17.Особливості перехідних процесів при розмиканні вітки з індуктивністю та замиканні вітки з ємністю.
- •18.Операторний метод розрахунку перехідних процесів.
- •19.3Акони Ома та Кірхгофа в операторній формі.
- •20.Внутрішні е.Р.С. В колах з перехідним процесом.
- •21.Операторна схема заміщення кола.
- •22.Формула розкладу і її застосування при розрахунку перехідних процесів.
- •23.Нелінійні елементи, їх класифікація, і застосування.
- •24.Статичні і диференційні опори.
16.Знаходження сталих інтегрування в класичному методі розрахунку перехідних процесів.
Перехідні процеси в нелінійних електричних ланцюгах описуються нелінійними диференціальними рівняннями, загальних методів інтегрування яких не існує. На нелінійні кола не поширюється принцип суперпозиції, тому засновані на ньому методи, зокрема класичний або з використанням інтеграла Дюамеля, для розрахунку даних ланцюгів не застосовні.
Аналіз перехідних режимів в електричних ланцюгах вимагає використання динамічних характеристик нелінійних елементів, які, в свою чергу, залежать від відбуваються в них динамічних процесів і, отже, в загальному випадку наперед невідомі. Зазначене спочатку обумовлює в тій чи іншій мірі наближений характер розрахунку перехідних процесів.
Перехідний процес в нелінійній ланцюга може характеризуватися змінною швидкістю його протікання в різні інтервали часу. Тому поняття постійної часу в загальному випадку не можна застосувати для оцінки інтенсивності протікання динамічного режиму.
Відсутність спільності підходу до інтегрування нелінійних диференціальних рівнянь зумовило наявність в математиці великого числа різноманітних методів їх вирішення, націлених на різні типи рівнянь. Стосовно до завдань електротехніки всі методи розрахунку по своїй суті можуть бути розділені на три групи:
- Аналітичні методи, що припускають або аналітичний вираз характеристик нелінійних елементів, або їх кусочно-лінійну апроксимацію;
- Графічні методи, основними операціями в яких є графічні побудови, часто супроводжувані допоміжними обчислювальними етапами;
- Чисельні методи, засновані на заміні диференціальних рівнянь алгебраїчними для збільшень змінних за відповідні інтервали часу.
17.Особливості перехідних процесів при розмиканні вітки з індуктивністю та замиканні вітки з ємністю.
18.Операторний метод розрахунку перехідних процесів.
Сутність
операторного методу полягає в тому, що
функції
![]() дійсної
змінної t, яку називають оригіналом,
ставиться у відповідність функція
дійсної
змінної t, яку називають оригіналом,
ставиться у відповідність функція
![]() комплексної
змінної
комплексної
змінної
![]() ,
яку називають
зображенням. В результаті цього похідні
та інтеграли від оригіналів замінюються
алгебраїчними функціями від відповідних
зображень (диференціювання замінюється
множенням на оператор р, а інтегрування
- діленням на нього), що в свою чергу
визначає перехід від системи
інтегро-диференціальних рівнянь до
системи алгебраїчних рівнянь щодо
зображень шуканих змінних . При вирішенні
цих рівнянь знаходяться зображення і
далі шляхом зворотного переходу -
оригінали. Найважливішим моментом при
цьому в практичному плані є необхідність
визначення тільки незалежних початкових
умов, що істотно полегшує розрахунок
перехідних процесів в ланцюгах високого
порядку в порівнянні з класичним методом.
,
яку називають
зображенням. В результаті цього похідні
та інтеграли від оригіналів замінюються
алгебраїчними функціями від відповідних
зображень (диференціювання замінюється
множенням на оператор р, а інтегрування
- діленням на нього), що в свою чергу
визначає перехід від системи
інтегро-диференціальних рівнянь до
системи алгебраїчних рівнянь щодо
зображень шуканих змінних . При вирішенні
цих рівнянь знаходяться зображення і
далі шляхом зворотного переходу -
оригінали. Найважливішим моментом при
цьому в практичному плані є необхідність
визначення тільки незалежних початкових
умов, що істотно полегшує розрахунок
перехідних процесів в ланцюгах високого
порядку в порівнянні з класичним методом.
Зображення заданої функції визначається відповідно з прямим перетворенням Лапласа:
|
У скороченою записи відповідність між зображенням і оригіналом позначається, як:
|
Слід
зазначити, що якщо оригінал
збільшується з ростом t, то для збіжності
інтеграла (1) необхідно більш швидке
спадання модуля
![]() .
Функції, з якими зустрічаються на
практиці при розрахунку перехідних
процесів, цій умові задовольняють. В
якості прикладу в табл. 1 наведено
зображення деяких характерних функцій,
що часто зустрічаються при аналізі
нестаціонарних режимів.
.
Функції, з якими зустрічаються на
практиці при розрахунку перехідних
процесів, цій умові задовольняють. В
якості прикладу в табл. 1 наведено
зображення деяких характерних функцій,
що часто зустрічаються при аналізі
нестаціонарних режимів.
Таблиця 1. Зображення типових функцій
Оригінал |
А |
|
|
|
|
|
Зображення |
|
|
|
|
|
|
Деякі властивості зображень
Зображення суми функцій дорівнює сумі зображень доданків:
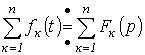
При множенні оригіналу на коефіцієнт на той же коефіцієнт множиться зображення:
![]()
З використанням цих властивостей і даних табл. 1, можна показати, наприклад, що
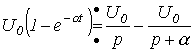
Зображення похідної та інтеграла
У
курсі математики доводиться, що якщо
![]() ,
то
,
то
![]() ,
де
,
де
![]() - початкове
значення функції.
- початкове
значення функції.
Таким чином, для напруги на індуктивному елементі можна записати
![]()
або при нульових початкових умовах
![]() .
.
Звідси операторний опір котушки індуктивності
![]()
Аналогічно
для інтеграла: якщо
![]() ,
то
,
то
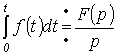 .
.
З урахуванням ненульових початкових умов для напруги на конденсаторі можна записати:
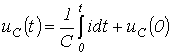
Тоді,
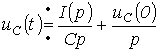
або при нульових початкових умовах
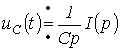 ,
,
звідки операторний опір конденсатора
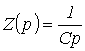 .
.

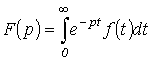 (1)
(1)