- •Задание на курсовой проект студента
- •Календарный план
- •1 Анализ предметной области
- •2 Агентно-ориентированная организация процесса проектирования
- •3 Постановка задачи
- •4 Входная и выходная информация
- •5 Математическое описание задачи
- •6 Предложенный алгоритм решения задачи
- •7 Описание программы
- •7.1 Используемые технические средства, вызов и загрузка
- •7.2 Описание классов и объектов программной среды
- •Приложение а Экранная форма программы
- •Приложение б.
- •Приложение в.
3 Постановка задачи
Разработать и исследовать работу в среде MathLab имитационной модели «Поведение мобильного агента в мультиагентной среде».
4 Входная и выходная информация
К входным данным относится:
а) интервал времени, через который приходят звонки абоненту;
б) интервал времени, который соединённые абоненты используют для передачи информации;
в) состояние мобильного счёта абонента(не остаточного);
г) вероятность совершения звонка, и его вероятность на соединение.
К выходным данным следует отнести информацию, выводимую в процессе функционирования процесса моделирования:
а) количество обслуженных абонентов мобильной сетью;
б) общая сумма минут, использованная абонентом, так и абонентами вместе;
в) количество успешных соединений.
г) прибыль мобильных операторов в общем.
5 Математическое описание задачи
Система может быть представлена в виде схемы массового обслуживания. Дадим описание диной схемы.
Задачи массового обслуживания возникают в тех случаях, когда условия на выполнение работы поступают в случайные моменты времени, а выполнение этих работ и производятся одним или несколькими обслуживающими приспособлениями. Длительность обслуживания отдельных заявок является случайной.
Устройство, способное в любой момент времени обслуживать лишь одну заявку, называется каналом обслуживания. Характерной особенностью задач массового обслуживания есть возникновения несоответствия между скоростью поступления заявок и скоростью обслуживания, вследствие чего или оказываются такими, что простаивают обслуженные приборы, или образовывается очередь на обслуживание. Поэтому принципиальный интерес представляют следующие характеристики СМО:
длина очереди в разные моменты времени;
общая продолжительность нахождения заявки в системе обслуживания;
частное времени, на протяжении которого обслуживающие приборы не были заняты.
Для получения математической модели СМО необходимо иметь:
описание входного потока заявок;
описание способа, которым выполняется обслуживание;
описание дисциплины очереди, т.е. указание того, чином заявки поступают из очереди на обслуживание.
Одним из основных подходов, которые используются при построении математических моделей процессов функционирования систем, есть безперервно-стохастичний подход. Особенности этого подхода выражаются в использовании как типичных математических схем систем массового обслуживания (англ. queuing system).
Схемы массового обслуживания является классом математических схем, разработанных в теории массового обслуживания и разных применениях для формализации процессов функционирования систем, которые по сути своей є процессами обслуживания.
Процесс обслуживания может быть разным по своей физической природе: процессы функционирования экономических, производственных, технических и др. систем, например: потоки поставок продукции некоторому предприятию, потоки деталей и комплектующих изделий на сборочном конвейере цеха, заявки на обработку информации ЭВМ от отдаленных терминалов и т.д.
При этом характерной для работы таких объектов есть случайное появление заявок на обслуживание и завершение обслуживания в случайные моменты времени, т.е. стохастичний характер процесса их функционирование.
В любом элементарном
акте обслуживания можно выделить две
основные составу: ожидание обслуживания
заявкой и собственное обслуживание
заявки. Это можно изобразить в виде
некоторого
![]() -го
прибора обслуживания
-го
прибора обслуживания![]() (рис.1), что
(рис.1), что![]() состоит
из накопителя заявок
состоит
из накопителя заявок![]() , в котором одновременно может находиться
, в котором одновременно может находиться![]() заявок, где
заявок, где![]()
![]()
![]()





![]()
![]()
![]()
![]()



Рис.5.1. Прибор обслуживания заявок.
Потоком событий называется последовательность событий, которые происходят одна за другой в некоторые случайные моменты времени.
Обычно при
моделировании разных систем относительно
элементарного канала обслуживания
![]() можно считать, что поток заявок
можно считать, что поток заявок![]() ,
т.е. интервалы времени между моментами
появления заявок на входе
,
т.е. интервалы времени между моментами
появления заявок на входе![]() , образовывают подмножество неуправляемых
сменных, а поток обслуживания
, образовывают подмножество неуправляемых
сменных, а поток обслуживания![]() , т.е. интервалы времени между началом
и окончанием обслуживания заявки,
образовывает подмножество управляемых
сменных
, т.е. интервалы времени между началом
и окончанием обслуживания заявки,
образовывает подмножество управляемых
сменных![]() .
.
В данной работе
рассматривается случай одного канала,
на который поступает поток требований
с интенсивностью
![]() .
Интенсивность обслуживания равная
.
Интенсивность обслуживания равная![]() .
Достоверность
.
Достоверность![]() того, что система находится в возможности
того, что система находится в возможности![]() в момент времени
в момент времени![]() , тогда равные:
, тогда равные:
![]() ,
где
,
где
![]()
Значение
![]() найдем из соотношение:
найдем из соотношение:
![]()
и
имеет смысл только при
![]() .
Используя формулу суммы бесконечной
нисходящей геометрической прогрессии,
получаем:
.
Используя формулу суммы бесконечной
нисходящей геометрической прогрессии,
получаем:
![]()
С учетом этого
выражения
![]() принимает вид:
принимает вид:
![]() ,
где
,
где
![]()
Основными характеристиками в системе есть средняя длина очереди и среднее время ожидания обслуживания.
Среднее число заявок, которые находятся в системе обслуживания
![]()
Учитывая, что:
![]()
находим:
![]() .
.
Можно также найти
среднее число заявок
![]() ,
которые проходят обслуживание. Поскольку
число заявок, которые находятся на
обслуживании, равное нулю, если канал
свободный, и единицы, в сдаче случаев,
то
,
которые проходят обслуживание. Поскольку
число заявок, которые находятся на
обслуживании, равное нулю, если канал
свободный, и единицы, в сдаче случаев,
то
![]()
Разность между
![]() и дает среднюю длину очереди
и дает среднюю длину очереди
![]()
Учитывая среднее время обслуживания одной заявки получаем выражение:
![]() .
.
Система «Остановка маршрутного такси» представляет собой типичную систему массового обслуживания. Каналами обслуживания есть маршрутные таксе, которые ждут наполнения, транзактами - пассажиры и такси, которое прибывало на остановку. Доступность канала отвечает наличию пустой маршрутки на конечной остановке. Схема данной системы одноканальная и однофазная, поскольку существует только один маршрут и чтобы достаться города не надо пересаживаться на другой вид транспорта. Периоды прихода пассажиров и прибытие маршрутных такси покоряют нормальному закону распределения с математическими ожиданиями возле 8.00 и 17.00 и дисперсией приблизительно в 1 ч.
Данный закон распределения выражается формулой:
|
|
(4.1) |
где t - время моделирования,
m - математическое ожидание,
![]() –дисперсия.
–дисперсия.
В графическом виде данный закон можно представить следующим графиком:
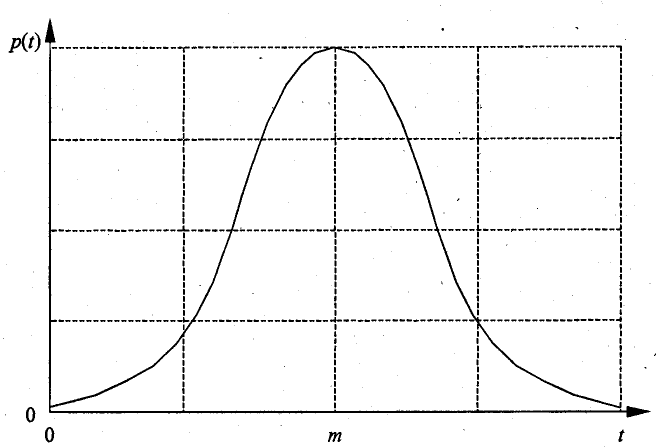
Рис.5.2 Нормальный закон распределения.