
- •Обратите внимание:
- •Архитектура пк
- •Модули bios
- •Железо компьютера (Hard).
- •Газодинамические функции
- •Математическая обработка результатов экспериментов
- •Расчет нестационарного температурного состояния правильных тел.
- •Расчет конечной температуры теплоносителей.
- •Построение поверхностей с помощью excel.
- •Однополостной гиперболоид
- •Поверхность состояния веществ в 2-хфазной области.
- •Решение обратной задачи – нахождение λ по q(λ)
- •Найти значения λ по методу Тунакова-Корабельникова
Расчет нестационарного температурного состояния правильных тел.
Краткая теория
Одномерное тело (бесконечные пластина и цилиндр, шар) с одинаковой температурой во всех точках, равной t/, в начальный момент времени τ0 погружается в жидкость с неизменной температурой tж . Коэффициент теплоотдачи на поверхности тела (для пластины с обеих боковых сторон) одинаков и постоянен.
Если за начало отсчета температуры
принять температуру окружающей среды
tж и избыточную температуру стенки
обозначить
![]() то дифференциальное уравнение
теплопроводности для твердых тел:
то дифференциальное уравнение
теплопроводности для твердых тел:
![]() , (1)
, (1)
а при рассмотрении относительно только
одной координаты принимает вид
![]()
Граничные условия: при х = δ
![]()
Начальное условие: при τ = 0
![]()
При этом температуры тела на поверхности tс и в плоскости симметрии t0 для любого момента времени определяются из следующих соотношений:
![]() и
и
![]()
где t/ - начальная температура по всему сечению тела.
Пример распределения температур по толщине плоской стенки во времени
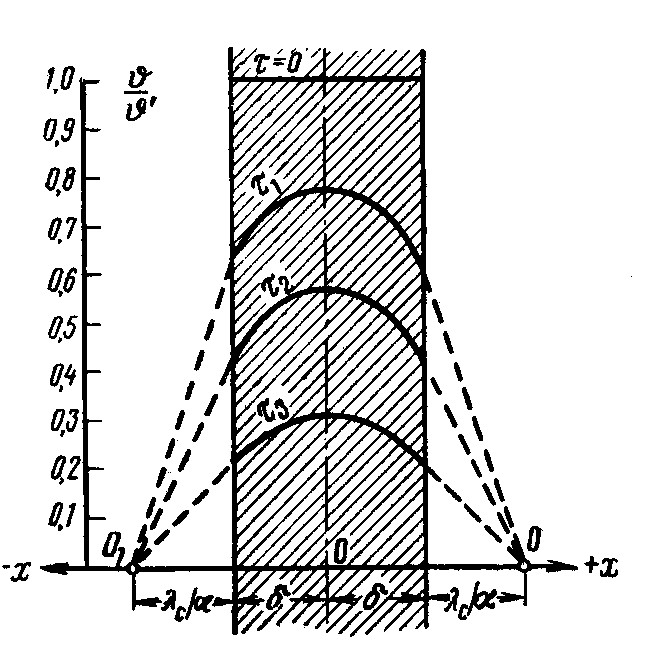
Рис. 2. Изменение температурного поля в плоской неограниченной стенке
от времени при охлаждении.
Безразмерная температура тела
![]() является функцией безразмерной координаты
является функцией безразмерной координаты
![]() ,
числа Био
,
числа Био
![]() и числа Фурье
и числа Фурье
![]() , где х- текущая координата в
направлении теплового потока, м;
ℓ-характерный линейный размер тела, м;
λ – коэффициент теплопроводности,
Вт/м·К и а =
, где х- текущая координата в
направлении теплового потока, м;
ℓ-характерный линейный размер тела, м;
λ – коэффициент теплопроводности,
Вт/м·К и а =![]() - коэффициент температуропроводности
материала тела, м2/с.
- коэффициент температуропроводности
материала тела, м2/с.
Аналитическое решение уравнения теплопроводности при заданных начальных и граничных условиях запишется:
![]() (2)
(2)
Здесь А и U – некоторые функции от корней характеристических уравнений μn, а сами корни являются однозначной функцией критерия Био.
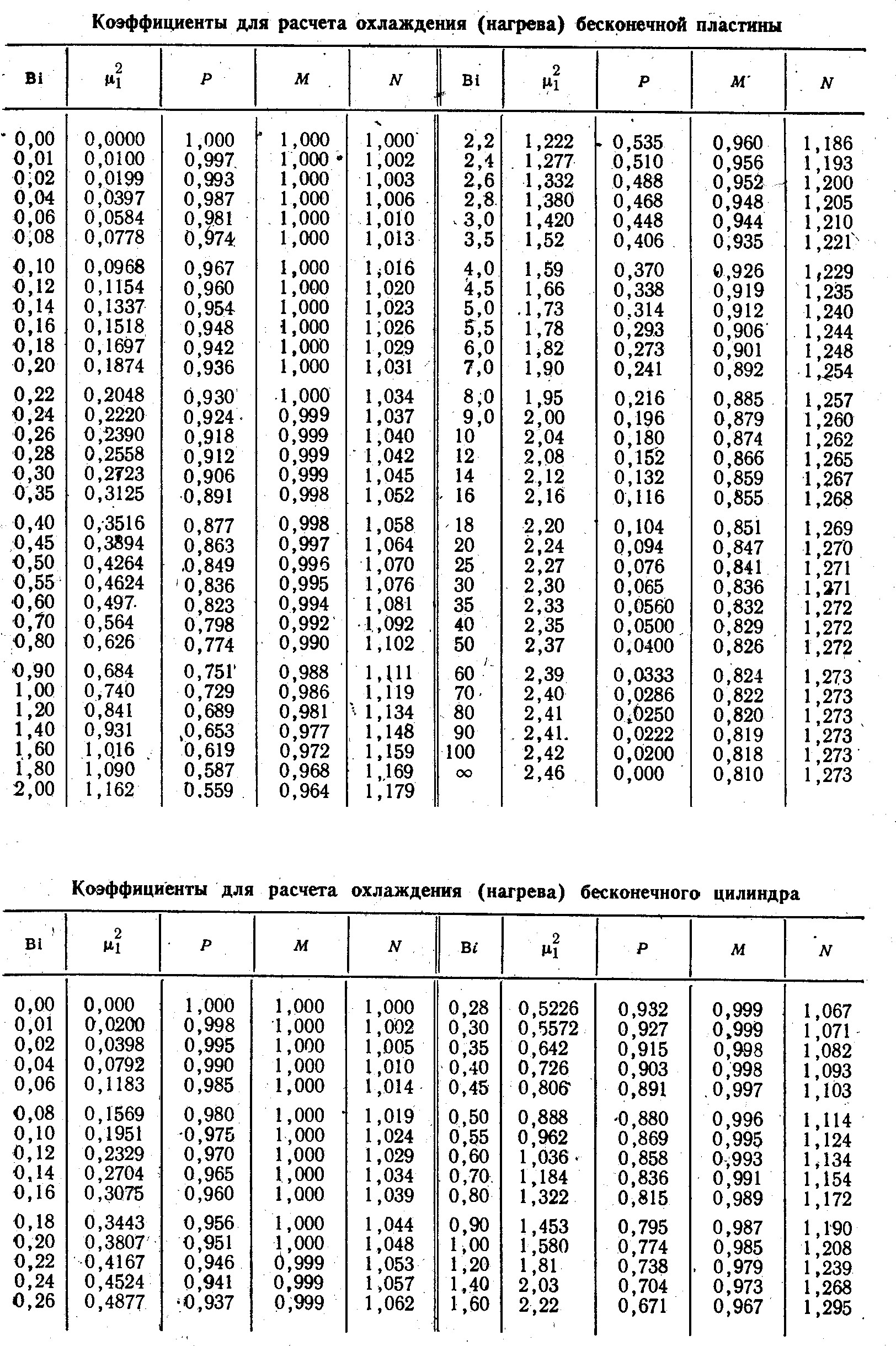
Таблица 1.

В таблице 1 приведены: вид характеристических
уравнений и соотношения для расчета
функций А(μn) и
![]() для случая охлаждения (нагрева)
бесконечной пластины, бесконечного
цилиндра и шара. Через J0
и J1 обозначены
функции Бесселя первого рода нулевого
и первого порядка (функции приведены в
табл.2). Начало координат расположено
на средней плоскости для пластины, на
оси для цилиндра и в центре для шара.
Решение (2) может быть использовано для
бесконечной пластины в случае, если
одна из боковых плоскостей имеет
абсолютную теплоизоляцию. В этом случае
начало координат необходимо поместить
на теплоизолированной стенке и в качестве
характерного размера принять всю толщину
стенки 2δ.
для случая охлаждения (нагрева)
бесконечной пластины, бесконечного
цилиндра и шара. Через J0
и J1 обозначены
функции Бесселя первого рода нулевого
и первого порядка (функции приведены в
табл.2). Начало координат расположено
на средней плоскости для пластины, на
оси для цилиндра и в центре для шара.
Решение (2) может быть использовано для
бесконечной пластины в случае, если
одна из боковых плоскостей имеет
абсолютную теплоизоляцию. В этом случае
начало координат необходимо поместить
на теплоизолированной стенке и в качестве
характерного размера принять всю толщину
стенки 2δ.
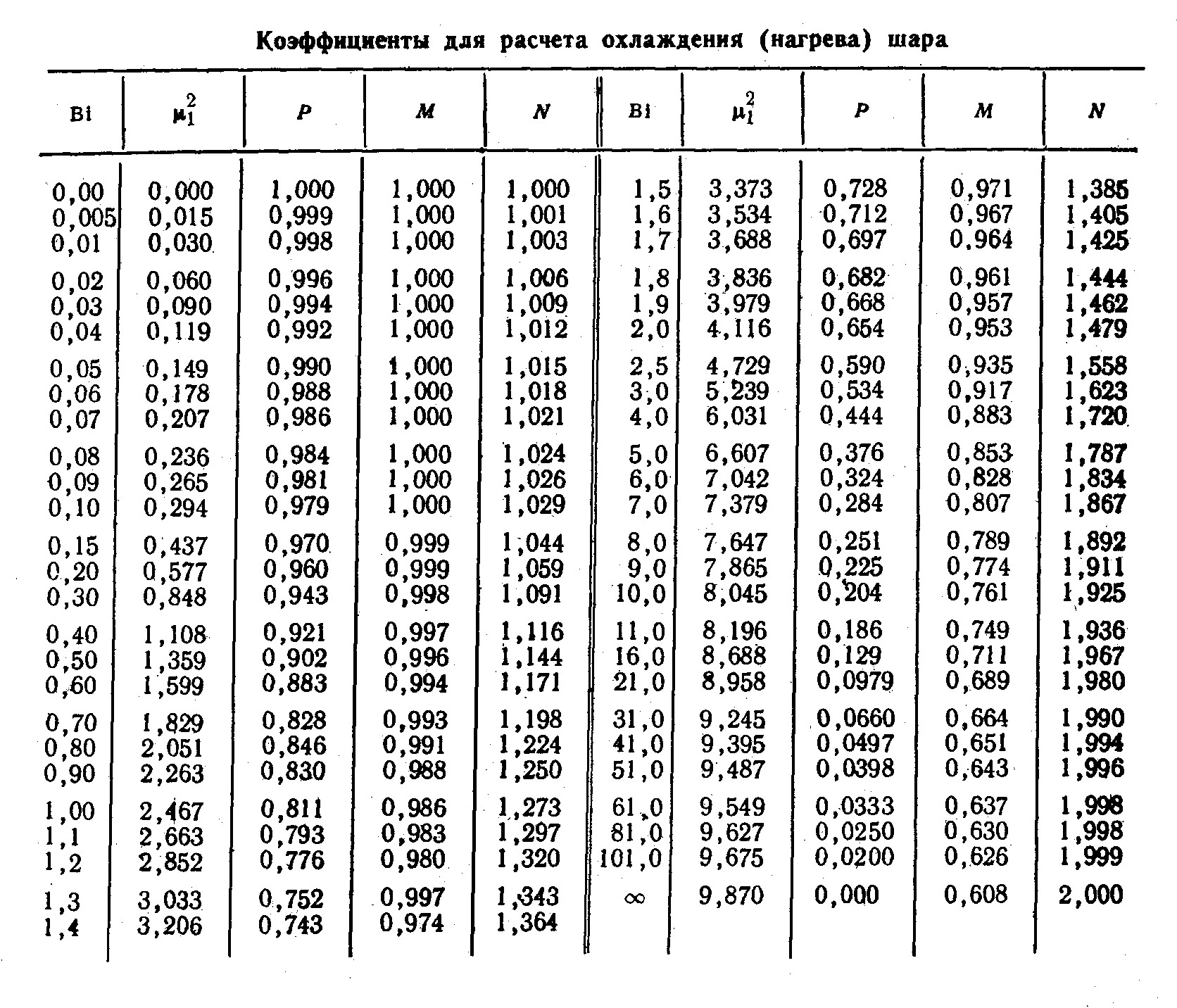
Первые шесть корней характеристических уравнений из таблицы 1 приведены в таблицах №№ 2 – 5.
При Fo>0,3 ряд (2) оказывается настолько быстро сходящимся, что для практических целей достаточно ограничиться первым членом (с погрешностью не выше 1%).
![]() (3)
(3)
Так для плоской пластины общий вид решения
![]() (3а)
(3а)
а для практических целей решение записывается
![]() (3/а)
(3/а)
Здесь
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Координата точки О на оси х расположена на расстоянии λст/αж , м.
Для расчетов применяют вспомогательные таблицы, включающие так называемые частные корни решения характеристического уравнения , обозначаемые обычно μ. Как отмечено выше, точное решение содержит набор частных решений, отличающихся значениями корней решения μn. Выше отмечено, что для практических целей применяют уравнения (3), включающие только первый член с коэффициентом μ1. Само значение μ1 зависит от критерия Bi и приводится в специальных таблицах.
Произвести расчет безразмерной
температуры
![]() в четырех точках с координатами
в четырех точках с координатами
![]() =0,
1/3, 2/3 и 1,0 для следующих значений Bi
0,01, 0,05 , 0,1 , 0,5 , 1,0 , 5 и 10 , Fo в зависимости
от варианта и построить график безразмерных
температур по Био для
=0
и
=1
=0,
1/3, 2/3 и 1,0 для следующих значений Bi
0,01, 0,05 , 0,1 , 0,5 , 1,0 , 5 и 10 , Fo в зависимости
от варианта и построить график безразмерных
температур по Био для
=0
и
=1
Варианты заданий для расчета
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
17 |
19 |
20 |
21 |
Fo =20 |
Fo=30 |
Fo= 50 |
||||||||||||||||||
РАСЧЕТ ТЕПЛООБМЕННИКОВ
Теплообменные аппараты находят широкое применение в энергетике и других областях народного хозяйства. Основной смысл этих устройств – передача тепловой энергии от теплоносителя с высоким уровнем входной температуры теплоносителю с более низким уровнем температуры.
Баланс теплового потока в теплообменнике записывается:
![]() (*)
(*)
- количество тепла, отданное горячим теплоносителем;
![]() (**)
(**)
- количество тепла, воспринятое холодным теплоносителем.
- ∆Q – потери тепла в окружающую среду;
- G1 и G2 массовые расходы теплоносителей в единицу времени;
- δi1 и δi2 –изменение энтальпии теплоносителей;
- ср1 и ср2 –теплоемкости теплоносителей;
- t/1 и t//1 – температуры горячего теплоносителя на входе и выходе из аппарата;
- t/2 и t//2 – температуры холодного теплоносителя на входе и выходе из аппарата.
Основные свойства теплоносителей объединяют в понятие водяного эквивалента каждого из теплоносителей. Его обозначают латинской буквой W.
W1=G1ср1 – водяной эквивалент первого теплоносителя
W2=G2ср2 – водяной эквивалент второго теплоносителя.
Значения температурных напоров в теплообменниках зависит от типа течения теплоносителей. Применяют следующие типы прямоток и противоток, а также перекрестный ток. Схематически изменения этих температур изображаются:
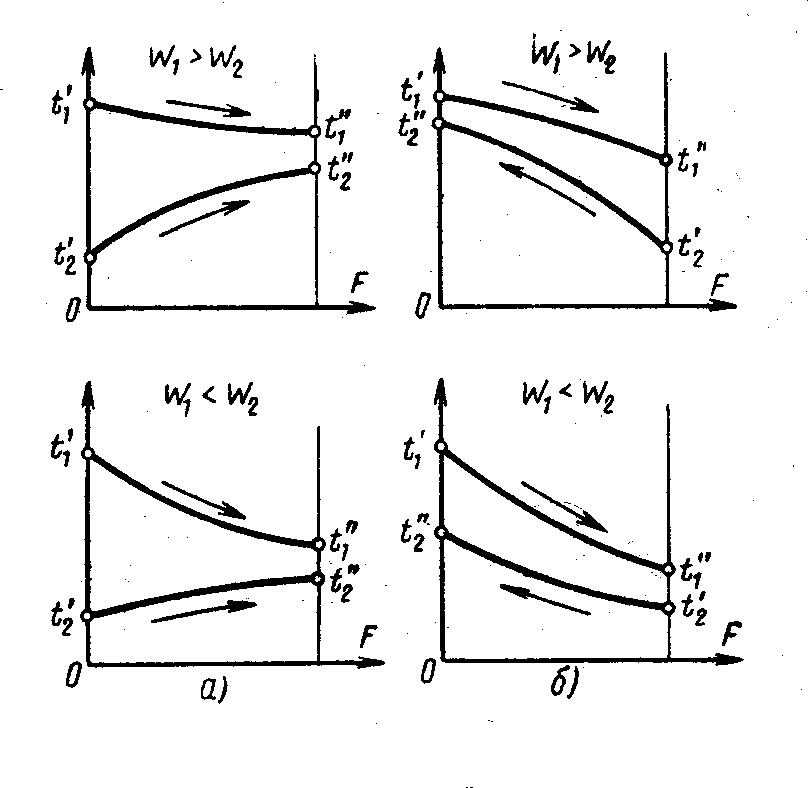
Характер изменения температур теплоносителей
при прямотоке (а) и противотоке (б).
