VII. Площадь треугольника

VII.1 Теоретическая карта № 7

Рисунок 173.

1.

2.

3. ,

где .

4. , где ,

r– радиус окружности, вписанной в

треугольник.

5. , где R – радиус окружности,

описанной около треугольника.

6. Если a=b=c, то .

Рисунок 174.

7. , где - угол

между медианами и .

Рисунок 175.

∆АВС: С=90⁰.

8.

9. ,

где r – радиус вписанной,

R – радиус описанной окружности.

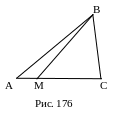Рисунок 176.

10. .

11. Если ∆А₁В₁С₁~∆АВС с

коэффициентом подобия k,

то

VII.2. Доказательства утверждений теоретической карты № 7

Доказательства следующих утверждений проводятся в учебниках [4] и [9].

1: [4, с.121], [9, с.219]. 2: [4, с.242], [9, с. 219]. 3: [9, с. 125].

4, 5: [9, с.222]. 8,10: [4, с.122].

Формула (6) тривиально получается из формулы (2). Её полезно помнить.

Формула (9) доказана в теоретической карте №6, а формула (10) – в теоретической карте № 1. Выведем формулу (7).

7.

Д ано: ∆АВС, АМ, ВD – медианы.

АМ=m_a, BD=m_b.

Доказать: .

Доказательство.

(теоретическая карта №5).

VII.3. Задачи к теоретической карте №7

№1. Найти площадь треугольника.

1.	2.
4. 7.	5.	6.
	8. В	9 30° . А В С
10.	11.	12.

Рис. 178

№2. Вычислить площадь равнобедренного треугольника, если длина его высоты, проведенной к боковой стороне, равна 12 см, а длина основания равна 15 см.

П лан решения.

1. КС.

2. ∆АКС∆BDС.

3. ВD.

4. S_∆АBС.

Ответ: 75 см².

Используемые факты из теоретической карты: 1.

№3. Диагонали разбивают трапецию на четыре треугольника. Доказать, что треугольники, прилежащие к её боковым сторонам равновелики.

П лан доказательства.

1. ОВ∙АО = ОС∙ОD.

2.

Используемые факты из теоретической карты: 2.

№4. В треугольнике АВС даны три стороны АВ=26, ВС=30, АС=28. Определить часть площади этого треугольника, заключенную между высотой и биссектрисой, проведенными из вершины В.

П лан решения.

1. S_∆ABC

2. BH.

3. AH.

4. LA.

5. LH.

6. S_∆LHB Ответ: 36.

Используемые факты из теоретической карты: 1, 3.

№5. Стороны треугольника 13 см, 14 см и 15 см. Определить радиус окружности, которая имеет центр на средней стороне и касается двух других сторон.

План решения.

1. S_∆ABC .

2. BH.

3. ОВ – биссектриса.

4. ОС.

5. S_∆ОBC .

6. ОК = r.

Ответ: 6 см.

Используемые факты из теоретической карты: 1, 3.

№6. Доказать, что сумма расстояний от любой точки, взятой внутри правильного треугольника, до его сторон равна 3r, где r – радиус вписанной в этот треугольник окружности.

План доказательства.

1. S_∆ABC = (р₁+р₂+р₃)∙а.

2. S_∆ABC=

3. р₁+р₂+р₃=3r

Используемые факты из теоретической карты: 1, 4.

№7. В треугольник вписан круг радиуса 4 см. Одна из сторон треугольника разделена точкой касания на части, равные 6 см и 8 см. Найти длины двух других сторон.

П лан решения.

1.

2. sin

3. AL.

4. Выразить S_∆ABC через BL.

5. Выразить P_∆ABC через BL.

6. Выразить S_∆ABC через радиус вписанного

круга.

7. BL из равенства площадей (4) и (6).

8. АВ. 9. ВС.

Ответ: 13 см и 15 см.

Используемые факты из теоретической карты: 2, 4.

№8. Стороны треугольника ABC равны 20 см, 34 см и 42 см. Найти отношение площадей вписанного и описанного кругов.

План решения.

1. S_∆ABC. 2. R. 3. p_∆ABC. 4. r. 5. Ответ:

Используемые факты из теоретической карты: 3, 4,5.

№9. Доказать, что для всякого треугольника имеет место равенство где r – радиус описанной окружности.

План доказательства.

1. 2. 3. 4.

Используемые факты из теоретической карты: 1, 4.

№10. Через середину стороны правильного треугольника проведена прямая, образующая с этой стороной угол α. Найти отношение площадей тех частей, на которые эта прямая разбивает треугольник.

П лан решения.

Пусть сторона данного треугольника равна а.

1. 2. sin 3. РМ. 4. S_∆PBM.

5. S_∆ABC. 6. S_APMC. 7.

Ответ: 2 сtg α + 1.

Используемые факты из теоретической карты: 2, 6.

№11. В треугольнике АВС проведена медиана ВD. Найти отношение радиуса окружности, описанной около треугольника АВD, к радиусу окружности, вписанной в треугольник АВС, если АВ=2, АС=6 и

План решения.

1. АD. 2. S_∆АВD. 3.ВD.

4. R_∆АВD. 5. ВС. 6. р_∆АВС.

7. S_∆АВС. 8. r_∆АВC. 9. R_∆АВD: r_∆АВC.

Ответ:

Используемые факты из теоретической карты: 2. 4, 5.

№12. Площадь треугольника равна 16 см², медианы m_a и m_b равны соответственно 6 см и 4 см. Доказать, что эти медианы перпендикулярны.

План доказательства.

1. Выразить площадь данного треугольника через медианы m_a и m_b.

2. Найти синус угла между медианами.

3. m_a m_b.

Используемые факты из теоретической карты: 7.

№13. Площадь равнобедренного треугольника равна S, а угол между медианами, проведенными к боковым сторонам, равен α. Найти основание треугольника.

П лан решения.

1. АА₁=СС₁. 2. АО=ОС. 3.

4. Выразить АО через АА₁.

5.Выразить АК через через АА₁.

6. Выразить АС через через АА₁.

7. Выразить АА₁ из формулы площади S данного

треугольника.

8. Подставить в формулу (6) выражение АА₁ через S.

Ответ:

Используемые факты из теоретической карты: 7.

№14. Периметр прямоугольного треугольника равен 2р, а гипотенуза равна с. Определить площадь круга, вписанного в этот треугольник.

План решения.

1. Выразить площадь треугольника через полупериметр и радиус вписанного круга.

2. Выразить площадь треугольника через гипотенузу и радиус вписанного круга.

3. Составить уравнение и решить его относительно r.

4. S_кр. Ответ: .

Используемые факты из теоретической карты: 4, 9.

№15. Высота, опущенная на гипотенузу прямоугольного треугольника, делит его на два треугольника, площади которых 6 и 54. Найти гипотенузу.

П лан решения.

1. ∆AСD∆CBD.

2. Найти к– коэффициент подобия

треугольников AСD и CBD.

3. DC=3AD.

4. AD. 5. DC. 6. BD. 7. AВ.

Ответ: 20. Используемые факты из теоретической карты: 8, 11.

№16. Найти острые углы прямоугольного треугольника, если известно, что отношение радиуса описанной около этого треугольника окружности к радиусу вписанной в него окружности равно 1+ .

П лан решения.

1. Выразить АС через R и sinA.

2. Выразить S_∆ABC через R и sin2A.

3. Выразить S_∆ABC через R и r.

4. Составить равенство площадей (2), (3).

5. Вычислить из равенства (4) sin2A.

6. 2А. 7. А. 8. В. Ответ: 30°, 60° Используемые факты из теоретической карты: 2, 9.

№17. Данный параллелограмм разделить на три равновеликие части прямыми, выходящими из одной вершины.

Д ополнительные построения.

1. BD.

2. L: L AD и AL:LD=2:1.

3. K: К DC и DK:KC: 1·2.

План решения.

1. S_∆АВL= S_∆ABD = S_ABCD.

2. S_∆ВKC= S_∆CBD = S_ABCD. 3. S_BLDK = S_ABCD.

Используемые факты из теоретической карты: 10.

№18. Через середину высоты равнобедренного треугольника проведены две прямые, соединяющие ее с вершинами основания. Какую часть площади треугольника составляет каждая из 6 частей, на которые эти прямые и высота разбивают треугольник?

Д ополнительное построение: DPAL.

План решения.

Пусть S_∆AВC =S

1. S_∆АOD = S_∆DOC = S. 2. BL: LC= .

3. S_∆OLC = 2 S_∆BOL. 4. S_∆BOС== S.

5. S_∆BOL= 6. S_∆OLC= .

Ответ: ; ; .

Используемые факты из теоретической карты: 10.

№19. Через середину Е высоты BD равнобедренного треугольника АВС (АВ=ВС) проведена прямая MN, параллельная AB (точка M принадлежит АС, точка N принадлежит ВС). Найти площадь треугольника CMN, если площадь треугольника АВС равна 32.

Д ополнительное построение: DP||MN.

План решения.

1. АМ = MD.

2. AD = DC.

3. - коэффициент подобия ∆CMN и ∆CBA.

4. S_∆CMN.

Ответ: 18.

Используемые факты из теоретической карты: 11.

№20. В треугольнике АВС, площадь которого равна 40 см², точка D делит сторону ВС в отношении BD:DC= 3:2. Отрезок AD пересекает медиану BK в точке Е. Найти площадь четырехугольника EDKC.

Д ополнительное построение: KN АD.

План решения.

1. S_∆KBC . 2. BN:NC. 3. S_∆KNC.

4. S_∆KBN. 5. BD:ВN. 6. S_∆BED.

7. S_EDNK. 8. S_EDCK.

Ответ: 11 см².

Используемые факты из теоретической карты: 10, 11.