
- •1.Плоскость комплексных чисел. Модуль, аргумент комплексного числа. Тригонометрическая форма записи комплексного числа.
- •2. Предел последовательности комплексных чисел.
- •3. Числовые ряды с комплексными членами.
- •4. Понятие функции комплексной переменной. Примеры.
- •Линейная ф-ция. Ее геометрический смысл.
- •7. Понятие производной функции комплексной переменной. Условия Коши-Римана.
- •8. Геометрический смысл модуля и аргумента производной. Понятие конформного отображения.
- •9. Показательная ф-ция и ее св-ва.
- •10. Логарифмическая функция и ее свойства.
- •Свойства логарифмической функции:
- •Свойства главного логарифма:
- •11. Тригонометрические ф-ции.
- •12. Понятие интеграла от функции комплексной переменной. Условия существования интеграла от функции комплексной переменной.
- •Свойства интегралов:
- •13. Интегральная теорема Коши.
- •14. Первооброзная. Формула Ньютона-Лейбница.
- •15. Интегральная формула Коши.
- •16.Понятие функционального ряда. Равномерная сходимость функциональных рядов.
- •17. Степенные ряды.
- •18. Аналитическая ф-ция. Разложение в ряд.
- •19. Теорема единственности.
- •20. Аналитическое продолжение.
- •21. Теорема Лиувилля.
- •22. Нули аналитической функции.
- •23. Ряд Лорана. Теор. Лорана.
- •24. Устранимые особые точки.
- •25. Полюсы функции комплексной переменной.
- •Необходимость.
- •Достаточность.
- •26. Существенно особые точки функции комплексной переменной. Теорема Сохоцкого-Вейерштрасса.
- •Достаточность.
- •27. Вычет функции. Теорема о вычетах.
- •28. Понятие логарифмического вычета. Принцип аргумента.
- •29. Теорема Руше.
- •30. Основная теорема алгебры.
15. Интегральная формула Коши.
Теорема(интегральная формула Коши).
Пусть
функция f(z)
аналитична в односвязной области D
и на ее границе Г. Тогда для любой точки
![]() справедливо равенство:
справедливо равенство: ![]()
Док-во.
Пусть
-произвольная
точка. Выберем ![]() Так как функция f(z)
аналитична в точке а,то она в ней
непрерывна. Следовательно, для выбранного
Так как функция f(z)
аналитична в точке а,то она в ней
непрерывна. Следовательно, для выбранного
![]() найдется
такое что для всех
найдется
такое что для всех ![]() таких, что
таких, что ![]() выполняется неравенство
выполняется неравенство ![]()
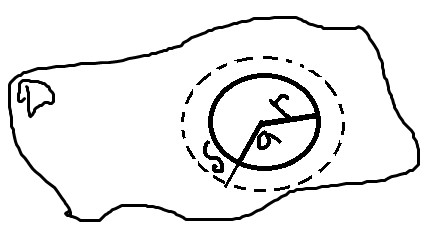 Рассмотрим
круг k1(a,r)
такой что
Рассмотрим
круг k1(a,r)
такой что ![]() Обозначим границу этого круга через
Обозначим границу этого круга через
![]() Рассмотрим функцию
Рассмотрим функцию ![]() она аналитична в области D,
за исключением точки a.
Значит,она аналитична в 2связной области,
полученой из области D
исключением круга k1(a,r).
Тогда по следствию из теоремы Коши:
она аналитична в области D,
за исключением точки a.
Значит,она аналитична в 2связной области,
полученой из области D
исключением круга k1(a,r).
Тогда по следствию из теоремы Коши:
![]()
Покажем, что последний интеграл равен f(a).

Покажем,
что ![]() равно нулю. Для этого оценим его по
модулю.
равно нулю. Для этого оценим его по
модулю.
![]()
![]()
Замечание 1. Из формулы коши следует, что если функция f(z) аналитична в области D и на ее границе, то она однозначно определяется через свои значения на границе Г области D.
Этот
факт отображают следующим образом: ![]()
Замечание2.
Если точка a
лежит во внешности контура Г, то ![]()
Пример.
![]() граница области D.
граница области D.

(график:единичная окружности заштрих.внутри)
16.Понятие функционального ряда. Равномерная сходимость функциональных рядов.
Пусть задана последовательность функций комплексного переменного z. f1(z),f2(z),…fn(z)..определенных на множестве D
Опр.
Функциональным
рядом называется символ вида
f1(z)+f2(z)+…+fn(z)+…
или ![]()
Опр. n-й частичной суммой называется функция Sn(z)= f1(z)+f2(z)+…+fn(z)
Рассмотрим
точку z0
области D,
тода функциональному ряду ставится в
соответствие числовой ряд
f1(z0)+f2(z0)+…+fn(z0)+…=
![]()
Тогда если этот числовой ряд сходится то z0 называется точкой сходимости.
Множество E всех точек сходимости функционального ряда называется областью сходимости функционального ряда.
Опр.
Функция S(z)
определенная на области E
для которой справедливо равенство ![]()
![]() называется суммой функционального
ряда.
называется суммой функционального
ряда.
Опр. Функциональный ряд f1(z)+f2(z)+…+fn(z)+…= называется равномерно сходящимся на множестве M если выполняются условия.
Сходится к функции S(z) на M

Теорема Критерий Коши равномерной сходимости
Функциональный
ряд
сходится равномерно к функции S(z)
на множестве М тогда и только тогда,
когда ![]()
Теорема. Признак Вейерштрасса
Пусть
дан функциональный ряд ![]() и для всех
и для всех ![]() существует сходящийся знакоположительный
ряд
существует сходящийся знакоположительный
ряд ![]() такой что
такой что ![]() тогда данный функциональный ряд сходится
сходится равномерно на множестве M.
тогда данный функциональный ряд сходится
сходится равномерно на множестве M.
Свойства равномерно сходящихся рядов.
Теорема. Если функциональный ряд сходится равномерно на M и функции fn(z) непрерывны на этом множестве то сумма этого ряда является непрерывной функцией на М.
Теорема. Пусть функциональный ряд сходится равномерно на спрямляемой кривой Г и каждая функция fn(z) непрерывны на Г тогда этот ряд можно почленно интегрировать вдоль кривой Г

Теорема. . Пусть функциональный ряд сходится равномерно в области D и функции fn(z) аналитичны в этой области, тогда сумма ряда S(z) также аналитична в области D, причем справедливо равентство

