- •1.Плоскость комплексных чисел. Модуль, аргумент комплексного числа. Тригонометрическая форма записи комплексного числа.
- •2. Предел последовательности комплексных чисел.
- •3. Числовые ряды с комплексными членами.
- •4. Понятие функции комплексной переменной. Примеры.
- •Линейная ф-ция. Ее геометрический смысл.
- •7. Понятие производной функции комплексной переменной. Условия Коши-Римана.
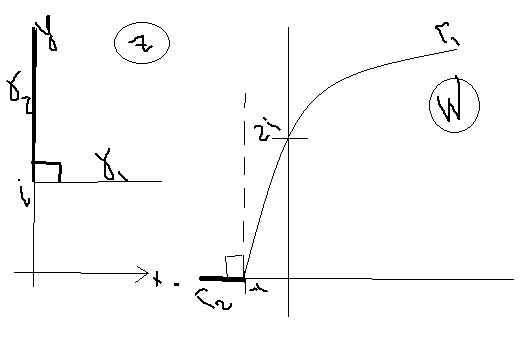
- •8. Геометрический смысл модуля и аргумента производной. Понятие конформного отображения.
- •9. Показательная ф-ция и ее св-ва.
- •10. Логарифмическая функция и ее свойства.
- •Свойства логарифмической функции:
- •Свойства главного логарифма:
- •11. Тригонометрические ф-ции.
- •12. Понятие интеграла от функции комплексной переменной. Условия существования интеграла от функции комплексной переменной.
- •Свойства интегралов:
- •13. Интегральная теорема Коши.
- •14. Первооброзная. Формула Ньютона-Лейбница.
- •15. Интегральная формула Коши.
- •16.Понятие функционального ряда. Равномерная сходимость функциональных рядов.
- •17. Степенные ряды.
- •18. Аналитическая ф-ция. Разложение в ряд.
- •19. Теорема единственности.
- •20. Аналитическое продолжение.
- •21. Теорема Лиувилля.
- •22. Нули аналитической функции.
- •23. Ряд Лорана. Теор. Лорана.
- •24. Устранимые особые точки.
- •25. Полюсы функции комплексной переменной.
- •Необходимость.
- •Достаточность.
- •26. Существенно особые точки функции комплексной переменной. Теорема Сохоцкого-Вейерштрасса.
- •Достаточность.
- •27. Вычет функции. Теорема о вычетах.
- •28. Понятие логарифмического вычета. Принцип аргумента.
- •29. Теорема Руше.
- •30. Основная теорема алгебры.
7. Понятие производной функции комплексной переменной. Условия Коши-Римана.
Пусть
однозначная функция ![]() определена в некой окрестности точки
определена в некой окрестности точки
![]()
ОПР.
Если существует конечный предел
отношения: ![]() то он называется производной функции
то он называется производной функции
![]() в точке
в точке ![]() .
.
![]()
Пр:
1) 
Замечание: В компл анализ переносится все правила диф-я теор. О произв.сложной и обратной функции.
Опр:
Функция ![]() называется дифференцируемой в точке
,
если ее приращение в этой точке можно
представить в виде:
называется дифференцируемой в точке
,
если ее приращение в этой точке можно
представить в виде: ![]() где
A=const,
где
A=const,
![]() б/м
при
б/м
при ![]() .
.
Замечание:
Как и на 1 курсе понятия дифференцирования
функции комплексного переменного
эквивалентно наличию производной
функции в точке
,
причем: ![]() .
.
Пр:
1)функция ![]() дифференцируема в
дифференцируема в ![]() 2)
2)![]() диф-ма в любой точке плоскости.
диф-ма в любой точке плоскости.
Теорема( Условие Коши-Римана)
Для
того чтобы функция ![]() была диф-ма в точке
была диф-ма в точке ![]() необходимо и достаточно, чтобы функции
U(x,y)
и V(x,y)
были диф-мы в точке
необходимо и достаточно, чтобы функции
U(x,y)
и V(x,y)
были диф-мы в точке ![]() и их частные производные в т. x0,y0
удовлетворяли условиям:
и их частные производные в т. x0,y0
удовлетворяли условиям:  .
.
Док-во: I. Необходимость.
Дано: ф-я диф-ма в точке z0; Доказать: (*)
![]() , введем обозначения:
, введем обозначения: ![]() ;
;
![]()
![]() );
);
![]()

Получим:
![]()
Из
последней системы следует,что ф-я U
диф-ма в точке ![]() причем
причем ![]() анологично V
в точке (x0,y0)
причем
анологично V
в точке (x0,y0)
причем ![]() ; докажем
ситему (*)
; докажем
ситему (*) ;
;
II.
Достаточность: Дано:![]() диф.; Док-ть:
диф. В т. z0
диф.; Док-ть:
диф. В т. z0
Т.к.
понятие диф-ти эквивалентно понятию
производной,то потребуется показать,что
сущ-ет производная ![]() .
.
Т.к.
![]() диф-ма
в т.
диф-ма
в т. ![]() то их полные приращения можно представить:
то их полные приращения можно представить:
![]() ;
; ![]()
Где
![]() тогда
тогда ![]()
Составим приращение ф-ии :
 ;
;
![]() ;
значит в т. z0
сущ.производная ф-ии
;
значит в т. z0
сущ.производная ф-ии ![]() , значит ф-я диф.ч.т.д.
, значит ф-я диф.ч.т.д.
Замечание:
Из теоремы следует, что при выполнении
(*) производная ф-ии ![]() может быть найдена на одной из формул
может быть найдена на одной из формул
![]() или же
или же ![]() .
.
Условие (*) – условие Кори-Римана.
Пр: выяснить в каких точках плоскости имеет пр-я ф-я
![]()
![]()
![]()
![]() ;
;
Ф-ии
U
и V
диф-е на всей плоскости ![]()
![]()
![]()
Замечание:
если ввести диф-е операторы (формальные
пр-е по ![]() по формулам
по формулам ![]() то ус-я Коши-Римана примет вид:
то ус-я Коши-Римана примет вид: ![]() произв.
произв. ![]()
Пр:
![]()
![]()
![]()
Пр:
![]()
![]() производной не имеет.
производной не имеет.
Опр: ф-я наз-я аналитической в т. z0, если она диф-ма в каждой точке некой окр-ти точки z0.
Замечание: из опр-я следует,что аналитич. В т. z0 ф-я будет аналитичной в каждой точке некой окр-ти т.z0.
Опр:
Ф-я
![]() аналитической
на мн-ве D,
если она аналит. В каждой т.,этого мн-ва.
аналитической
на мн-ве D,
если она аналит. В каждой т.,этого мн-ва.
Пр:
аналит:
![]() ; не аналит:
; не аналит: ![]()
8. Геометрический смысл модуля и аргумента производной. Понятие конформного отображения.
Пусть
функция
имеет производную в точке ![]() и при этом
и при этом ![]() Тогда
Тогда ![]()
![]()
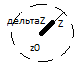 ;
;
![]()
![]()
![]()
При
достаточно близких ![]() яункция
,
имеющая в точке
яункция
,
имеющая в точке ![]() производную ведет себя почти как линейная
функция вида
производную ведет себя почти как линейная
функция вида ![]() Те функция
осуществляет преобразование подобия,
Те функция
осуществляет преобразование подобия,
![]() - отвечает за сжатие и растяжение,
- отвечает за сжатие и растяжение, ![]() - за перенос.
- за перенос.
Вспомним
Кривая
![]() называют
непрер,если функции
называют
непрер,если функции ![]() непрерывны
на
непрерывны
на ![]()
Кривая
называется гладкой, если ![]() диффер.при условии
диффер.при условии ![]() .
.
В
комлексной форме ![]() будет
непрерывна, если
будет
непрерывна, если ![]() -
непрерывны, как действительные функции
действительных переменных.
-
непрерывны, как действительные функции
действительных переменных.
Аналогично определяется гладкая кривая на комлексной плоскости.
Пр:
1. ![]()
![]() ;
2.
;
2. ![]()
![]() ;
;
Замечание:
Пусть функция ![]() - непрерывна в некоторой области D
и кривая
- непрерывна в некоторой области D
и кривая ![]() .
Тогда отображение осуществляемое
функцией
переведет кривую
.
Тогда отображение осуществляемое
функцией
переведет кривую ![]() в некоторую кривую
в некоторую кривую
![]() .
.![]()
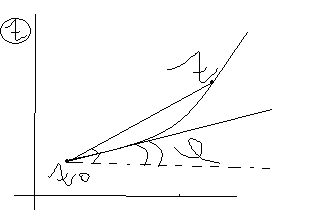
Пусть
задана функция
,
имеющая производную в точке ![]() Предположим, что из точки z0
выходит кривая гамма мал., имеющая
касательную в точке z0.
Рассмотрим произвольную точку z
принадлежащ.гамма мал. Тогда вектор
Предположим, что из точки z0
выходит кривая гамма мал., имеющая
касательную в точке z0.
Рассмотрим произвольную точку z
принадлежащ.гамма мал. Тогда вектор ![]() будет являтся ед.вектором секущей.
будет являтся ед.вектором секущей.
Получим
![]()
Тк
в точке
существует косательная, то ![]()
На
плоскости w
будет: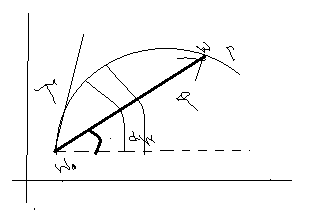 пусть
пусть
![]() является единич.вектором сукущей для
гамма больш.
является единич.вектором сукущей для
гамма больш.
Преобразуем
![]()
Перейдем
к пределу ![]()
Т.о.
в точке ![]() кривая гамма больш. Имеет касательную
для которой справедливо соотношение
кривая гамма больш. Имеет касательную
для которой справедливо соотношение

Т.о
при отображении
угол ![]() представляет собой угол поворота который
совершает касательная кривой. Т.е при
отображении
сохраняются углы между кривыми.
представляет собой угол поворота который
совершает касательная кривой. Т.е при
отображении
сохраняются углы между кривыми.
Опр: Отображение сохраняющее углы называют конформными.
Выясним геометрический смысл модуля производной
![]() ;
;
Т.о
модуль
есть коэффициент деформации отображения
![]()
Пр:
Найти образы гамма мал.1 и гамма мал.2
при отображении ![]()
 ;
решение
;
решение


![]()