7. Понятие производной функции комплексной переменной. Условия Коши-Римана.

Пусть однозначная функция определена в некой окрестности точки

ОПР. Если существует конечный предел отношения: то он называется производной функции в точке .

Пр: 1)

Замечание: В компл анализ переносится все правила диф-я теор. О произв.сложной и обратной функции.

Опр: Функция называется дифференцируемой в точке , если ее приращение в этой точке можно представить в виде: где A=const, б/м при .

Замечание: Как и на 1 курсе понятия дифференцирования функции комплексного переменного эквивалентно наличию производной функции в точке , причем: .

Пр: 1)функция дифференцируема в 2) диф-ма в любой точке плоскости.

Теорема( Условие Коши-Римана)

Для того чтобы функция была диф-ма в точке необходимо и достаточно, чтобы функции U(x,y) и V(x,y) были диф-мы в точке и их частные производные в т. x0,y0 удовлетворяли условиям: .

Док-во: I. Необходимость.

Дано: ф-я диф-ма в точке z0; Доказать: (*)

, введем обозначения: ; );

Получим:

Из последней системы следует,что ф-я U диф-ма в точке причем анологично V в точке (x0,y0) причем ; докажем ситему (*) ;

II. Достаточность: Дано: диф.; Док-ть: диф. В т. z0

Т.к. понятие диф-ти эквивалентно понятию производной,то потребуется показать,что сущ-ет производная .

Т.к. диф-ма в т. то их полные приращения можно представить:

_;

Где тогда

Составим приращение ф-ии :

;

; значит в т. z0 сущ.производная ф-ии , значит ф-я диф.ч.т.д.

Замечание: Из теоремы следует, что при выполнении (*) производная ф-ии может быть найдена на одной из формул или же .

Условие (*) – условие Кори-Римана.

Пр: выяснить в каких точках плоскости имеет пр-я ф-я

;

Ф-ии U и V диф-е на всей плоскости

Замечание: если ввести диф-е операторы (формальные пр-е по по формулам то ус-я Коши-Римана примет вид: произв.

Пр:

Пр: производной не имеет.

Опр: ф-я наз-я аналитической в т. z0, если она диф-ма в каждой точке некой окр-ти точки z0.

Замечание: из опр-я следует,что аналитич. В т. z0 ф-я будет аналитичной в каждой точке некой окр-ти т.z0.

Опр: Ф-я аналитической на мн-ве D, если она аналит. В каждой т.,этого мн-ва.

Пр: аналит: ; не аналит:

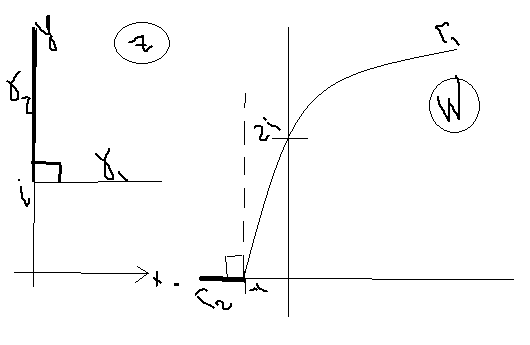
8. Геометрический смысл модуля и аргумента производной. Понятие конформного отображения.

Пусть функция имеет производную в точке и при этом Тогда ;

При достаточно близких яункция , имеющая в точке производную ведет себя почти как линейная функция вида Те функция осуществляет преобразование подобия, - отвечает за сжатие и растяжение, - за перенос.

Вспомним

Кривая называют непрер,если функции непрерывны на

Кривая называется гладкой, если диффер.при условии .

В комлексной форме будет непрерывна, если - непрерывны, как действительные функции действительных переменных.

Аналогично определяется гладкая кривая на комлексной плоскости.

Пр: 1. ; 2. ;

Замечание: Пусть функция - непрерывна в некоторой области D и кривая . Тогда отображение осуществляемое функцией переведет кривую в некоторую кривую .

Пусть задана функция , имеющая производную в точке Предположим, что из точки z0 выходит кривая гамма мал., имеющая касательную в точке z0. Рассмотрим произвольную точку z принадлежащ.гамма мал. Тогда вектор будет являтся ед.вектором секущей.

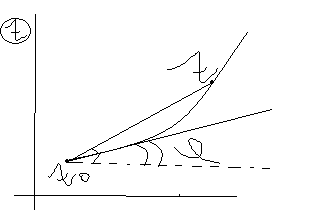
Получим

Тк в точке существует косательная, то

На плоскости w будет: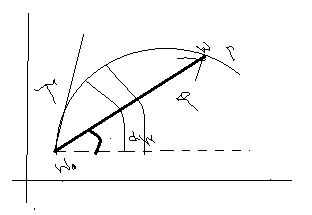 пусть является единич.вектором сукущей для гамма больш.

Преобразуем

Перейдем к пределу

Т.о. в точке кривая гамма больш. Имеет касательную для которой справедливо соотношение

Т.о при отображении угол представляет собой угол поворота который совершает касательная кривой. Т.е при отображении сохраняются углы между кривыми.

Опр: Отображение сохраняющее углы называют конформными.

Выясним геометрический смысл модуля производной

;

Т.о модуль есть коэффициент деформации отображения

Пр: Найти образы гамма мал.1 и гамма мал.2 при отображении

1. ; решение