
- •1.Плоскость комплексных чисел. Модуль, аргумент комплексного числа. Тригонометрическая форма записи комплексного числа.
- •2. Предел последовательности комплексных чисел.
- •3. Числовые ряды с комплексными членами.
- •4. Понятие функции комплексной переменной. Примеры.
- •Линейная ф-ция. Ее геометрический смысл.
- •7. Понятие производной функции комплексной переменной. Условия Коши-Римана.
- •8. Геометрический смысл модуля и аргумента производной. Понятие конформного отображения.
- •9. Показательная ф-ция и ее св-ва.
- •10. Логарифмическая функция и ее свойства.
- •Свойства логарифмической функции:
- •Свойства главного логарифма:
- •11. Тригонометрические ф-ции.
- •12. Понятие интеграла от функции комплексной переменной. Условия существования интеграла от функции комплексной переменной.
- •Свойства интегралов:
- •13. Интегральная теорема Коши.
- •14. Первооброзная. Формула Ньютона-Лейбница.
- •15. Интегральная формула Коши.
- •16.Понятие функционального ряда. Равномерная сходимость функциональных рядов.
- •17. Степенные ряды.
- •18. Аналитическая ф-ция. Разложение в ряд.
- •19. Теорема единственности.
- •20. Аналитическое продолжение.
- •21. Теорема Лиувилля.
- •22. Нули аналитической функции.
- •23. Ряд Лорана. Теор. Лорана.
- •24. Устранимые особые точки.
- •25. Полюсы функции комплексной переменной.
- •Необходимость.
- •Достаточность.
- •26. Существенно особые точки функции комплексной переменной. Теорема Сохоцкого-Вейерштрасса.
- •Достаточность.
- •27. Вычет функции. Теорема о вычетах.
- •28. Понятие логарифмического вычета. Принцип аргумента.
- •29. Теорема Руше.
- •30. Основная теорема алгебры.
27. Вычет функции. Теорема о вычетах.
Опр:
Пусть a
изолир-я ок-ть фун-ии
,
вычетом фун-ии
в точке а наз-ся:
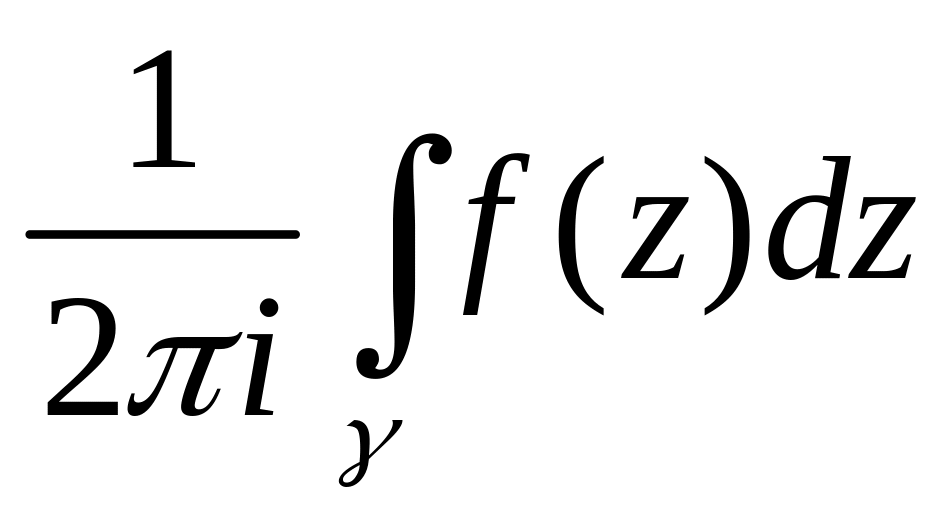 где
где
![]() некая
ок-ть целиком лежащая в проколотой ок-ти
точки а, не содержащих других особых
точек
некая
ок-ть целиком лежащая в проколотой ок-ти
точки а, не содержащих других особых
точек
Обозначается
вычет:

Пр:

Теорема
(Вычет фун-кции
![]() является ее разложением в ряд Лорана
в окр-ти точки а)
является ее разложением в ряд Лорана
в окр-ти точки а)
Пр:
![]()

Следствие:
1)
![]()
2)Если
точка а полюс 1-го порядка ф-ии
,
![]()
![]()
3)
Если точка а полюс к-го порядка ф-ии,
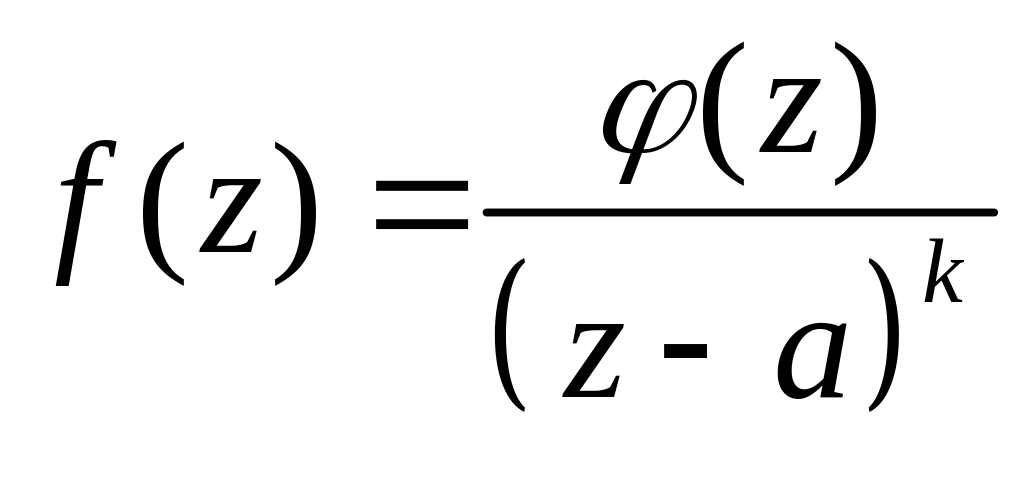 то
вычет ф-ии будет авен:
то
вычет ф-ии будет авен:


Замечание:
![]()
4)Если
в некой окр-ти точки а фун-я
представлена в виде
![]() где
где
![]() аналитична, причем
аналитична, причем
![]()
![]()
![]()
Док-во:
Функция
имеет в точке а 0 первого порядка
Пр:

Найти вычет
![]()
с![]()
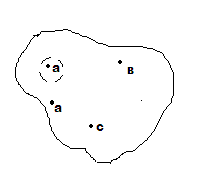
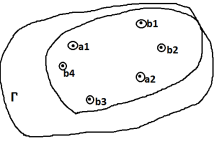
Теорема о вычетах пусть ф-ция f(z) аналит.в обл. D за искл. конечного числа особ. т. ak к=1,…,n. Пусть контур Г целиком лежит в обл. D и не проходит ни через одну из особ. точек ф-ции f(z), причем все особ. т. лежат внутри контура .
док-во поведем n окр. |z-ak|=rk так чтобы они целиком лежали внутри контура Г так, что бы внутри каждой из этих окр. была токлько одна особая т. ф-ции и они не имели общих точек - γk. ч.т.д.
28. Понятие логарифмического вычета. Принцип аргумента.
Пусть
функции ![]() аналитичны в проколотой окрестности
точки
аналитичны в проколотой окрестности
точки ![]()
Опр:
Логарифмическим вычетом функции
в точке
называется вычет ее логарифмической
производной ![]()
Пусть – ноль порядка
 для
функции
для
функции  т.е.
т.е.
 где
где
 аналит.
аналит.


![]()
Пусть
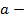 полюс порядка
полюс порядка  для функции
для функции  где
-
аналитична и
где
-
аналитична и  .
.
![]()
![]()
Точка
![]() является
полюсом первого порядка.
является
полюсом первого порядка.
![]() ;
;
Теор::
Пусть функция
аналитична в D
за исключением конечного числа полюсов
![]() кратностей
кратностей ![]() соответственно и обращающихся в нуль
в точках
соответственно и обращающихся в нуль
в точках ![]() кратностей
кратностей ![]() пусть контур
целиком лежит в области D
и охватывает все полюсы и нули функции
f(z),
тогда справедливо рав-во:
пусть контур
целиком лежит в области D
и охватывает все полюсы и нули функции
f(z),
тогда справедливо рав-во:

Док-во: По теореме о выч.
![]()
Пр:
![]()
![]() ;
;
![]() ;
;
– аналитична на всей плоскости P=0
![]()
 (график:един.окружность
с центром (1,0) на компл.плоскости);
(график:един.окружность
с центром (1,0) на компл.плоскости);
Геометрический смысл логарифмического вычета.
![]()
![]()
Будем считать точку z0 началом,концом контура Г.
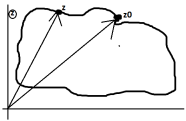
Пусть
точка z
проходит кривую Г начиная из точки z0в
положительном напрвлении. Тогда ![]() будет описывать на плоскости w
некоторую непрерывную кривую Г’ с
началом в точке
будет описывать на плоскости w
некоторую непрерывную кривую Г’ с
началом в точке ![]() замкнута.
замкнута.
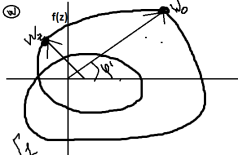
![]()
Пусть
аргумент точки w0
до начала обхода равен ![]() .
Обозначим аргумент конечной точки w0
.
Обозначим аргумент конечной точки w0
![]()
Вообще
говоря справедливо: ![]()
С
другой стороны: ![]()
Обозначим
![]()
Логарифмический
вычет будет равен изменению аргумента
функции f(z)
деленному на ![]() и умноженная на аргумент f(z)
!!!
дальше видимо пропущена строчка
и умноженная на аргумент f(z)
!!!
дальше видимо пропущена строчка
Теор: Пусть функция аналитична в D за исключением конечного числа полюсов кратностей соответственно и обращающихся в нуль в точках кратностей
Пусть
кривая L
целиком лежит в D
и охватывает все нули и полюсы функции
f(z),
тогда разность между числом нулей и
числом полюсов функции f(z)
равна делимому на 2![]() изменению аргумента функции f(z)
при обходе кривой L;
т.е
изменению аргумента функции f(z)
при обходе кривой L;
т.е ![]()
29. Теорема Руше.
Теорема:
Пусть функции ![]() аналитичны в области D
и контур L
целиком лежит в этой области, тогда если
на контуре L
выполняется неравенство
аналитичны в области D
и контур L
целиком лежит в этой области, тогда если
на контуре L
выполняется неравенство ![]() то функция
и функция
то функция
и функция ![]() имеют внутри контура L
одинаковое число нулей.
имеют внутри контура L
одинаковое число нулей.
(график: область D внутри которой замкнутая кривая(контур) L)
Док:
![]()
Применим принцип аргумента.
![]()
Рассмотрим последовательность слаг.
![]()
Значит
значения ![]() лежат внутри круга с центром в точке 1
радиуса 1.
лежат внутри круга с центром в точке 1
радиуса 1.
![]()
Значит
измен.вдоль ![]()
Т.о
изменение ![]()
Так
как функции ![]() аналитичны в области
аналитичны в области ![]() ,
то функция
не имеет полюсов. Т.о в силу принципа
аргумента
,
то функция
не имеет полюсов. Т.о в силу принципа
аргумента ![]() число нулей внутри контура L.
число нулей внутри контура L.
![]() тоесть
число нулей совпадает.
тоесть
число нулей совпадает.
Пример: Определить количество корней уравнения.
![]() (график:единичная окружность на
компл.плоскости |z|=1)
(график:единичная окружность на
компл.плоскости |z|=1)
![]()
