1.Плоскость комплексных чисел. Модуль, аргумент комплексного числа. Тригонометрическая форма записи комплексного числа.
Рассмотрим на плоскости систему координат XoY и поставим в соответствие каждому комплексному числу z=x+iy точку с координатами (x,y)
Каждой точке можно поставить в соответствие её радиус-вектор поэтому комплексные числа можно интерпретировать как векторы на плоскости.
ОПР.
Модулем
комплексного числа z
называется длина радиус вектора его
изображающего т.е. 
ОПР. Аргументом комплексного числа z=x+iy называется угол, на который нужно повернуть положительную часть оси ОХ до ее совпадения с вектором, изображающим число z.Обозначается Argz
Число 0 не имеет аргумента.
ОПР. Главным аргументом комплексного числа z называется аргумент принадлежащий промежутку (-π;π) Обозначается argz.
Ось ОХ называется действительной осью, ось ОУ-мнимой.
Тригонометрическая форма записи комплексного числа.
Свойства модуля комплексного числа
Свойства аргумента
Arg(z1z2)=Argz1+Argz2
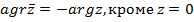
Тригонометрическая форма комплексного числа
Если рассмотреть на плоскости полярную систему координат то
2. Предел последовательности комплексных чисел.
На комплексной плоскости принято вводить Евклидову метрику, поэтому комплексная плоскость является метрическим пространством и для него справедливы все введенные ранее понятия, включающие понятие предела.
Опр: Говорят, что задана последовательность комплексных чисел, если каждому натуральному числу по некоторому правилу поставлено в соответствие единственное комплексное число.
Пр:
1. 
;
2. 
;
Замечание:
каждой последовательности комплексных
чисел 
можно поставить в соответствие две
последовательности действительных
чисел, представляющих собой действительную
и мнимую части членов данной
последовательности, те 
Пр:
Опр:
Комплексное число 
называется пределом последовательности
,
если 
.
Опр:
Замечание: Предел последовательности комплексных чисел обладает всеми свойствами пределов.
Пр: найти предел последовательности:
Теорема:
Пусть задана последовательность 
,
тогда 
в том и только в том случае, когда 
Теорема:
если 
Док-во:
Опр:
3. Числовые ряды с комплексными членами.
Пусть
задана последовательность комплексных
чисел 
Опр:
Числовым рядом называется символ вида:
при этом члены последовательности
называются членами этого ряда.
Опр:
Сумма n
первых членов ряда называется n-ой
частичной суммой 
Опр:
Числовой ряд называется сходящимся,
если существует конечный предел
последовательности его частичных сумм
в
противном случае называется расходящимся.
Заметим,
что 
где 
Таким образом сходимость числового
ряда эквивалентна сходимости 2ч числовых
рядов с действительными членами,
состоящими из действительных n-ми
частей исходного ряда.
Замечание: Числовые ряды в комплексном анализе обладают всеми свойствами числовых рядов.
Опр: Числовой ряд называется абсолютно сходящимся, если сходится ряд из модулей членов ряда.
Опр: Если ряд сходится, а из модулей расходится, то ряд называется условно сходящимся.
Пр: Исследовать на сходимость.
составим ряд из модулей. 
Воспользуемся признаком коши 
.