39.Нахождение интегралов вида Интеграл вида подстановкой или сводится к интегралу от рациональной функции относительно sint или cost.

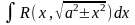_{находиться с помощью подстановки или}

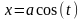
40.

41. Полные дифференциалы высших порядков от ФНП. Пусть функция f(x)- дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную

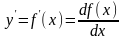
Если найти производную функции f(x), получим вторую производную функции f(x).

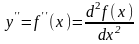
т.е. y = (y) или .

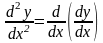Этот процесс можно продолжить и далее, находя производные степени n.

.

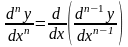42.Уравнения с разделяющимися переменными.Дифференциальное уравнение первого порядка в общем виде записывается так: F(x,y,y') = 0.(24.6) Если это уравнение разрешимо относительно у', то y'=f(x,y) (24.7) или dy-f(x,y)dx = 0. (24.8) Последнее уравнение является частным случаем уравнения. P(x,y)dx+Q(x,y)dy=0 (24.9).Задача Коши для дифференциального уравнения первого поряд­ка: найти решение у = у(х) уравнения (24.6), удовлетворяющее усло­вию у = уо при х = хo, или у(хo) = уо, (24.10)где хo, уо - заданные числа. Геометрически задача Коши означает сле­дующее: найти L интегральную линию, проходящую через точку Мo(хo, уо).Если в уравнении у' = f(x, у) функция f(x, у) и ее частная производная по у, непрерывны в некоторой области G плоскости Оху, содержащей точку Mo(xo, уо), то решение задачи Коши существует и являет­ся единственным. В этом случае через точку Mo(xo, уо) проходит един­ственная интегральная линия. Рассмотрим частный случай, а именно, ко­гда функции Р(х, у) и Q(x, у) представляют собой произведения функ­ции только от х на функцию только от у, т.е. Р(х, у) =f(x) (у), Q(x, у) =fi(x)1(y), в этом случае уравнение принимает вид f(x)(y)dx+f1(x)l(y)dy = 0. (24.11)Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если его можно привести к виду (24.11), где f(x), f1(x) - функции только от х,(у), ,1(у) - функ­ции только от у.Разделив почленно это уравнение на f1(х)(у) в предположении, что , f1(х)(у)=0 (24.12) получим уравнение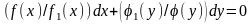 (24.13) Уравнение (24.13) называется уравнением с разделенными пере­менными.

43.Линейные дифференциальные уравнения первого порядка.

Линейным дифференциальным уравнением первого порядка на­зывается уравнение вида а(х)y' + b(х)у = с(х), (24.22) где у = у(х) - искомая функция; а(х), b(х), с(х) - заданные функции. Будем считать, что они непрерывны на отрезке [a, b], причем а(х) не равно 0. Поскольку а(х) не равно 0 при любом х[а, b], то данное уравнение можно переписать так: y'+p(x)y=f(x). (24.23)Решение уравнения будем искать в виде произведения двух функций v = v(x), u = u(х) - y = uv. (24,24) Так как у' = u'v + uv', то подстановка выражений для у и у' в уравнение (24.23) приводит его к виду u'v + uv' + p(x)uv =f(x), или u'v + u[v'+p(x)v]=f(x). (24.25) В качестве v выберем одну из функций, обращающих в нуль сумму в квадратных скобках, т.е. функцию, удовлетворяющую уравне­нию v'+p(x)v = 0. (24.26) С учетом (24.26) уравнение (24.25) принимает вид u'v =f(x).(24.27)

Уравнение (24.26) является уравнением с разделяющимися пе­ременными х и v, из него определяется функция v = v(x). Функция u = u(х) определяется из уравнения (24.27), которое при v = v(x) также является уравнением с разделяющимися переменными. Определив u = u(х) и v = v(x), по формуле (24.24) найдем у. 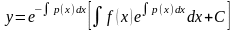(24.30)

44.Однородные дифференциальные уравнения первого порядка.Функция F(x, у) называется однородной измерения n, если при любом t выполняется тождество F(tx,ty)=tⁿF(x,y). (24.15) Дифференциальное уравнение первого порядка P(x,y)dx + Q(x,y)dy = 0 (24.16)называется однородным, если Р(х, у) и Q(x, у) - однородные функции одного и того же измерения n. В этом случае соотношение (24.15) принимает вид P(tx,ty)= tⁿP(x,y), Q(tx,ty)= tⁿQ(x,y).

Полагая в последних равенствах t = 1 :х, х не равно 0, получаем P(1,y/x)dx+Q(1,y/x)dy=0 (24.17)Введем новую переменную u по формуле u=y/x или y=ux (24.18) Поскольку в этом случае dy = udx + xdu, то уравнение (24.17) принимает вид P(l, u)dx + Q(l, u)(udx + xdu) =0, или [P(l,u) + uQ(l,u)]dx + xQ(l,u)du = 0. (24.19) Последнее уравнение является уравнением с разделяющимися переменными х, u; из него определяется u, а из формулы (24.18) - ис­комая функция у. .Если Ф(x,u,c) = 0 (24.20) - общий интеграл уравнения (24.19), то Ф(x,y/x,c)=0 (24.21) - общий интеграл уравнения (24.16).

45.Уравнение Бернулли является одним из наиболее известных нелинейных дифференциальных уравнений первого порядка. Оно записывается в виде

где a(x) и b(x) − непрерывные функции.  Если m = 0, то уравнение Бернулли становится линейным дифференциальным уравнением. В случае когдаm = 1, уравнение преобразуется в уравнение с разделяющимися переменными.  В общем случае, когда m ≠ 0, 1, уравнение Бернулли сводится к линейному дифференциальному уравнению с помощью подстановки

Новое дифференциальное уравнение для функции z(x) имеет вид

и может быть решено способами, описанными на странице Линейные дифференциальные уравнения первого порядка.