Раздел 5. Элементы аналитической геометрии

Тема 5.2. Уравнение прямой. Лекция 33.

Пересечение двух прямых.

Параллельность и перпендикулярность прямых.

Прямая линия.

Уравнение прямой. Мы знаем, что уравнение 1-й степени с 2-мя неизвестными вида

у = ах + b

выражается помощью координатных осей в виде прямой линии, которая образует с положительным направлением оси x угол α, определяемый равенством: tg α = а, и отсекает от оси у отрезок, равный b. Так как к такому виду может быть приведено всякое уравнение 1-й степени с 2-мя неизвестными х и у, то такое уравнение выражается при помощи координатных осей в виде прямой линии (почему оно и называется линейным уравнением).

Покажем теперь, что, обратно,  всякая прямая линия может быть выражена уравнением 1-й степени с двумя  неизвестными х и у.

Сначала допустим, что прямая АА' (черт. 1) проходит через начало координат О, образуя с Ох острый угол α.

Черт.1

Возьмем на этой прямой произвольную точку М, абсцисса которой есть х = ОВ и ордината у = МВ. Из треугольника ОМВ видно, что y = x tg α, или у = ах, если tg α обозначим а. Выведенное нами уравнение у = ах верно не только для точек полупрямой ОА, но и для точек полупрямой ОА'. Возьмем, напр., точку M', которой координаты будут: x = — ОВ', у = — M'В'. Из тр-ка ОВ'М' находим: M'B' = B'O tg α, т. е. — y = — x tg α, или y = x tg α. Таким образом, уравнение у = ах верно для всякой точки прямой АА'.

Теперь допустим, что прямая АА' проходит через начало координат, но образует с Ох не острый угол, а тупой α (черт. 2).

Черт.2

Если M есть какая-нибудь точка этой прямой, то ее абсцисса х = — ОВ и ордината у =MВ, и мы из тр-ка ОMВ находим:

MВ =ОВ tg MОВ,

т. е.

у = — x tg MОВ.

Но tg MOB = tg(180°—α) = — tg α; значит, у = — х( — tg α)= х tg α = ax, если по-прежнему обозначим tg α через а. Подобное же уравнение получим и для любой точки M, расположенной на ОА'.

Наконец, допустим, что дана прямая СС' или DD' (черт. 1 и 2), не проходящая через О, а отсекающая от оси у отрезок, равный b (или — b). Тогда, проведя через точку О вспомогательную прямую АА' || CC'(или || DD'), мы получим для этой прямой уравнение у = ах, где a = tg α. Но очевидно, что при одной и той же абсциссе х ординаты точек прямой СС' больше ординат точек прямой АА' на b, а прямой DD' меньше на b; значит, уравнение прямой СС' будет у = ах + b, а прямой DD' у = ах — b, где а есть по-прежнему тангенс угла, образованного прямой с положительным направлением оси х.

Частные случаи. 1) Если а = 0, т. е.   если данная прямая параллельна   оси х,  то уравнение   будет:   у = b.   Если она при этом сливается с осью х, то уравнение окажется:

у = 0.

2) Если данная прямая параллельна оси у и отсекает от оси х отрезок k, то уравнение такой прямой будет: х = к (ордината, как не входящая в уравнение, остается произвольной).

Уравнение  прямой,  проходящей  через данную точку.

Если прямая у = ах + b проходит через точку (x₁ , y₁  ), то мы должны иметь равенство

y₁ = аx₁ + b

Вычтя почленно это равенство из уравнения  у = ах + b, получим:

у — y₁ = а(х — x₁).

Что прямая, определяемая этим уравнением, действительно проходит через точку (x₁ , y₁  ), видно из уравнения непосредственно: подставив вместо х  и у соответственноy₁ иx₁ получим тождество: 0 = 0.

Угловой коэффициент а остается неопределенным, так как через одну точку может проходить бесчисленное множество прямых.

Примеры. Уравнение прямой, проходящей через:

точку (2,3) будет: у — 3 = а(х — 2); „ ( — 2,3)      „   у—3 = a(x + 2); „ ( — 2,—3)   „  у + 3 = а(х + 2); ,, (0,3)            ,,   у — 3 = ах;           ,,        (0,0)     „  у = ах.                

Уравнение прямой, проходящей через 2 данные точки.

Положим, что прямая:

у — y₁ = а(х — x₁),                                    (1)

проходящая через точку (x₁ , y₁ ), проходит еще через другую точку (x₂ , y₂ ). Тогда координаты этой другой точки должны удовлетворять уравнению прямой, и следовательно:

y₂ — y₁ = а (x₂ — x₁), откуда находим:

Мы  нашли   таким   образом  угловой   коэффициент  прямой, проходящей через 2 данные точки (x₁ , y₁ ) и (x₂ , y₂ ).

Теперь уравнение можно написать так:

что можно изобразить в таком удобном для запоминания виде:

Что прямая, удовлетворяющая этому уравнению, проходит через точки (x₁ , y₁ ) и (x₂ , y₂), видно из уравнения непосредственно; подставив вместо х и у соответственно x₁ , y₁ или x₂ , y₂получим тождества:

Пример. Уравнение прямой, проходящей через точки A (2, 3) и B(— 2, 1), будет:

что после упрощения дает: х — 2у = — 4.

Пример. Уравнение прямой, проходящей через точки А(1, 7) и В(-3, -1): Пример. Уравнение прямой, проходящей через точки В(-3, -1) и C(4,-2): Пример. Уравнение прямой, проходящей через точки А(1, 7) и C(4,-2):

Углом между прямыми A и B называется угол, на который надо повернуть первую прямую A вокруг точки пересечения этих прямых против движения часовой стрелки до совпадения ее со второй прямой B. Если две прямые заданы уравнениями с угловым коэффициентом

y = k₁x + B₁,         

y = k₂x + B₂,     

то угол между ними   определяется по формуле

     

Следует обратить внимание на то, что в числителе дроби из углового коэффициента второй прямой вычитается угловой коэффициент первой прямой.

Если уравнения прямой заданы в общем виде

A₁x + B₁y + C₁ = 0,         

A₂x + B₂y + C₂ = 0,     

угол между ними определяется по формуле

     

Параллельность и перпендикулярность прямых.

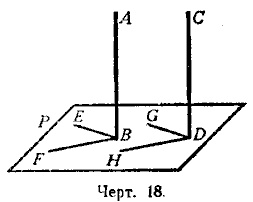
Параллельность прямых и плоскостей в пространстве и перпендикулярность прямой к плоскости находятся в некоторой зависимости. Именно наличие параллельности одних элементов влечёт за собой перпендикулярность других, и, обратно, из перпендикулярности одних элементов можно сделать заключение о параллельности других. Эта связь между параллельностью и перпендикулярностью прямых и плоскостей в пространстве выражается следующими теоремами. Теорема. Если плоскость (Р, черт. 18) перпендикулярна к одной из параллельных прямых (АВ), то она перпендикулярна и к другой (CD). Проведём через точку В на плоскости Р две какие-нибудь прямые ВЕ и BF, а через точку D проведём прямые DG и DH, соответственно параллельные прямым ВЕ и BF. Тогда будем иметь: / АВЕ = / CDG и / ABF = / CDH, как углы с параллельными сторонами. Но углы ABE и ABF прямые, так как АВ _|_ Р, значит, углы CDG и CDH также прямые. Следовательно, CD _|_Р . Обратная теорема. Если две прямые (АВ и СD, черт.19) перпендикулярны к одной и той же плоскости (Р), то они параллельны. Предположим противное, т. е. что прямые АВ и СD не параллельны. Проведём тогда через точку D прямую, параллельную АВ. При нашем предположении это будет какая-нибудь прямая DС1 , не сливающаяся с DС. Согласно прямой теореме прямая DС1 будет перпендикулярна к плоскости Р. Проведём через СD и С1D плоскость Q и возьмём линию её пересечения DЕ с плоскостью Р. Так как (на основании предыдущей теоремы)  С1D _|_ Р, то / С1DE прямой, а так как по условию СD _|_Р, то / СDЕ также прямой. Таким образом, окажется, что в плоскости Q к прямой DЕ из одной её точки D восставлены два перпендикуляра DС и DС1. Так как это невозможно, то нельзя допустить, чтобы прямые АВ и СD были нe параллельны. Теорема. Если прямая (ВВ1, черт. 20) перпендакулярна к одной из параллельных плоскостей (Р), то она перпендикулярна и к другой (Q). Проведём через прямую ВВ1 какие-нибудь две плоскости М и N, каждая из которых пересекается с Р и Q по параллельным прямым: одна — по параллельным прямым ВС и В1С1, другая—по параллельным прямым ВD и В1D1. Согласно условию прямая ВВ1перпендикулярна к прямым ВС и ВD; следовательно, она также перпендикулярна к параллельным им прямым В1С1 и В1D1 а потому перпендикулярна и к плоскости Q, на которой лежат прямые В1С1 и В1D1. Обратная теорема. Если две плоскости (Р и О, черт.21) перпендикулярны к одной и той же прямой (АВ), то они параллельны. Предположим противное, т. е. что плоскости Р и Q пересекаются. Возьмём на линии их пересечения какую-нибудь точку С и проведём плоскость R через С и прямую АВ. Плоскость R пересечёт плоскости Р и Q соответственно по прямым АС и ВС.  Так как АВ _|_ Р, то АВ _|_ АС, и так как АВ _|_ Q, то АВ _|_ ВС. Таким образом, в плоскости R мы будем иметь два перпендикуляра к прямой АВ, проходящих через одну и ту же точку С, перпендикуляры АС и ВС. Так как это невозможно, то предположение, что плоскости Р и Q пересекаются, неверно. Значит, они параллельны.