
- •1. Первообразная и ее свойства
- •3. Таблица интегралов.
- •2.Неопределенный интеграл и его свойства
- •4.Замена переменной в неопределенном интеграле
- •5. Интегрирование по частям в не опред. Интеграле
- •6. Интегрирование выраж содержащ квадратный трехчлен
- •7.Интегрирование простых правильных дробей
- •9.Интегрирование некоторых классов иррац функций
- •10.Интегрирование тригонометрических выражений
- •11. Определение определенного интеграла и его св-ва
- •12. Интеграл с переменным верхним пределом;производная по верхнему пределу
- •13.Формула Ньютона-Лейбница
- •14.Замена переменной в определенном интеграле
- •15.Интегрирование по частям в определенном интеграле
- •16.Геометрические приложения определенного интеграла
- •17.Несобственные интегралы по бесконечному промежутку интегрир от непрерывных функций.
- •18.Несобственные интегралы по конечному промежутку интегрирования от неограниченных функций.
- •19. Диффер уравн: опред, решение уравн, задача Коши, общ и частн решения, геом смысл решений
- •20.Диффер уравнен первого порядка с разделенными и разделяющ переменными
- •21.Лин диффер уравнения 1го порядка(методы Бернулли и Лагранжа, их решения)
- •22.Лин диффер уравн 2го порядка с пост коэфф, структура их общ решения
- •23. Структура решения лин неоднор дифф уравн 2го порядка
- •24.Нахождение частных реш лин неоднор диффер уравн 2го порядка с пост коэфф по виду правой части
- •25. Числовой ряд и его сумма; сход и расход ряды
- •26. Геометрический и гармонический ряды
- •27. Необходимые условия сходимости ряда
- •28.Полож ряды; признаки сравнен их сходимости
- •29.Предельный признак Даламбера
- •30.Предельный признак Коши
- •31.Интегральный признак Маклорена-Коши
- •32.Знакоперемен ряды, абсол и условная сходимости
- •33.Теорема Коши об абсол сход знакоперем ряда
- •34.Признак Лейбница знакочеред рядов
- •35.Теорема Абеля сходимости степенного ряда
- •36.Радиус сходим степенного ряда и его нахождение
- •37. Понятие о рядах Тейлора и Маклорена
- •39.Разложение в ряд Маклорена ф-ции cos X, sin X
24.Нахождение частных реш лин неоднор диффер уравн 2го порядка с пост коэфф по виду правой части
Рассмотрим
способы нахождения частного решения
неоднородного уравнения
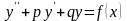 при специальных видах правой части
f(x).
при специальных видах правой части
f(x).
Пусть правая часть уравнения (8.1) имеет вид
f(x) = eσx Pn(x),(8.3)где σ – некоторое действительное число, называемое контрольным числом правой части уравнения (8.1), а Pn(x) = a0 + a1x + … + anxn (8.4) есть многочлен степени n ≥ 0 с действительными коэффициентами. При n = 0 (8.4) задаёт многочлен нулевой степени Pn(x) = a0 ≠ 0, который не нужно путать с так называемым нулевым многочленом – функцией, являющейся тождественным нулём.
Заметим, что при σ = 0 правая часть уравнения (8.1) будет представлять собой многочлен (8.4).
Пусть
правая часть уравнения (8.1) имеет вид
(8.3). Тогда а) если контрольное число σ
не является корнем характеристического
уравнения соответствующего приведённого
однородного уравнения, то частное
решение
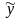 необходимо искать в виде у
= еσх
Qn(x);
(8.5) б) если σ является простым (однократным)
корнем характеристического уравнения
(7.2), то частное решение находят в виде
у
= хеσх
Qn(x);
(8.6)
необходимо искать в виде у
= еσх
Qn(x);
(8.5) б) если σ является простым (однократным)
корнем характеристического уравнения
(7.2), то частное решение находят в виде
у
= хеσх
Qn(x);
(8.6)
в) если σ является двукратным корнем характеристического уравнения (7.2), то частное решение надо искать в виде у = х2еσх Qn(x).(8.7)
В выражениях (8.5) – (8.7) многочлен Qn(x) есть многочлен такой же степени, что и многочлен Рn(x), стоящий в правой части (8.3), т.е. он имеет вид
Qn(x) = b0 + b1x + … + bnxn. (8.8)
Коэффициенты br (r = 0, 1, ..., n) многочлена (8.8) подлежат нахождению. Это делается следующим образом. Для соответствующей ситуации функции (8.5), (8.6), (8.7) и входящие в уравнение производные подставляются в (8.1). После этого сокращают на еσх и приравнивают коэффициенты при одинаковых степенях х слева и справа. Получится система алгебраических уравнений для нахождения коэффициентов br многочлена (8.8). Этот способ нахождения чисел br называют методом неопределённых коэффициентов.
Данный вывод о нахождении частных решений уравнения (8.1) относится и к случаю σ = 0, т.е. случаю, когда правая часть f(x) этого уравнения имеет вид (8.4). Тогда в ситуациях б) и в) можно было бы поступить иначе. В ситуации б) имеем q = 0 и можно понизить порядок уравнения, применяя подстановку z = y′. В ситуации в) имеем, что коэффициенты p и q равны нулю; тогда уравнение может быть решено интегрированием, т.к. оно имеет вид у′′ = Pn(x).
25. Числовой ряд и его сумма; сход и расход ряды
Определение 1. Выражение вида
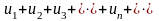 (6)
(6)
(в
краткой записи
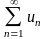 ),
состоящее из суммы членов бесконечной
числовой последовательности (5),
называется числовым
рядом (или
просто рядом).
),
состоящее из суммы членов бесконечной
числовой последовательности (5),
называется числовым
рядом (или
просто рядом).
Элементы
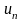 ,
из которых образовано выражение (6),
называют членами
данного ряда.
,
из которых образовано выражение (6),
называют членами
данного ряда.
В
основном
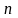 -й
член
задаётся для всех
единой аналитической формулой. Тогда
называют общим
членом ряда.
Ряд будет считаться заданным, если
будет указана формула его общего члена
.
-й
член
задаётся для всех
единой аналитической формулой. Тогда
называют общим
членом ряда.
Ряд будет считаться заданным, если
будет указана формула его общего члена
.
Определение
2.
Сумма первых
членов ряда (6) называется
-й
частичной суммой
ряда и обозначается через
 ,
т.е.
,
т.е. (7)
(7)
Очевидно,
что с увеличением
частичные суммы (7) расширяются до
формального ряда (6). Поскольку сложение
бесконечного множества чисел не
определено, то естественно будет назвать
суммой ряда (6) предел последовательности (8)
его частичных сумм. Известно, что любая
числовая последовательность либо
сходится (имеет конечный предел), либо
расходится (имеет пределом
(8)
его частичных сумм. Известно, что любая
числовая последовательность либо
сходится (имеет конечный предел), либо
расходится (имеет пределом
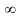 или вообще не имеет никакого предела
– ни конечного, ни бесконечного).
или вообще не имеет никакого предела
– ни конечного, ни бесконечного).
Определение
3.
Если существует конечный предел
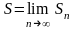 последовательности (8) частичных сумм
ряда (6), то этот предел называют суммой
этого ряда
(при этом
записывают
последовательности (8) частичных сумм
ряда (6), то этот предел называют суммой
этого ряда
(при этом
записывают
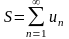 )
и говорят, что ряд сходится.
Если
)
и говорят, что ряд сходится.
Если
 или вообще не существует, то ряд
называется расходящимся.
или вообще не существует, то ряд
называется расходящимся.
Если
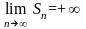 ,
то условно пишут
,
то условно пишут
 ;
соответственно
;
соответственно
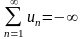 ,
если
,
если
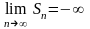 .
.
