
- •1. Первообразная и ее свойства
- •3. Таблица интегралов.
- •2.Неопределенный интеграл и его свойства
- •4.Замена переменной в неопределенном интеграле
- •5. Интегрирование по частям в не опред. Интеграле
- •6. Интегрирование выраж содержащ квадратный трехчлен
- •7.Интегрирование простых правильных дробей
- •9.Интегрирование некоторых классов иррац функций
- •10.Интегрирование тригонометрических выражений
- •11. Определение определенного интеграла и его св-ва
- •12. Интеграл с переменным верхним пределом;производная по верхнему пределу
- •13.Формула Ньютона-Лейбница
- •14.Замена переменной в определенном интеграле
- •15.Интегрирование по частям в определенном интеграле
- •16.Геометрические приложения определенного интеграла
- •17.Несобственные интегралы по бесконечному промежутку интегрир от непрерывных функций.
- •18.Несобственные интегралы по конечному промежутку интегрирования от неограниченных функций.
- •19. Диффер уравн: опред, решение уравн, задача Коши, общ и частн решения, геом смысл решений
- •20.Диффер уравнен первого порядка с разделенными и разделяющ переменными
- •21.Лин диффер уравнения 1го порядка(методы Бернулли и Лагранжа, их решения)
- •22.Лин диффер уравн 2го порядка с пост коэфф, структура их общ решения
- •23. Структура решения лин неоднор дифф уравн 2го порядка
- •24.Нахождение частных реш лин неоднор диффер уравн 2го порядка с пост коэфф по виду правой части
- •25. Числовой ряд и его сумма; сход и расход ряды
- •26. Геометрический и гармонический ряды
- •27. Необходимые условия сходимости ряда
- •28.Полож ряды; признаки сравнен их сходимости
- •29.Предельный признак Даламбера
- •30.Предельный признак Коши
- •31.Интегральный признак Маклорена-Коши
- •32.Знакоперемен ряды, абсол и условная сходимости
- •33.Теорема Коши об абсол сход знакоперем ряда
- •34.Признак Лейбница знакочеред рядов
- •35.Теорема Абеля сходимости степенного ряда
- •36.Радиус сходим степенного ряда и его нахождение
- •37. Понятие о рядах Тейлора и Маклорена
- •39.Разложение в ряд Маклорена ф-ции cos X, sin X
9.Интегрирование некоторых классов иррац функций
Далеко не каждая иррациональная функция может иметь интеграл, выраженный элементарными функциями. Для нахождения интеграла от иррациональной функции следует применить подстановку, которая позволит преобразовать функцию в рациональную, интеграл от которой может быть найден как известно всегда.
1.
Интегралы вида
 ,
где R-рациональная
функция,
,
где R-рациональная
функция,
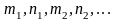 -целые
числа преобразуются в интегралы от
рациональных функций с помощью
подстановки
-целые
числа преобразуются в интегралы от
рациональных функций с помощью
подстановки
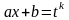 ,где
к-общий
,где
к-общий
знаменатель
дробей
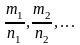
2.
Интегралы вида
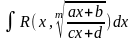 , где
, где
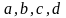 -некоторые
-некоторые
числа
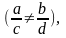 m-натуральное
число, преобразуются с помощью
m-натуральное
число, преобразуются с помощью
подстановки
 .
.
3.
Интегралы вида
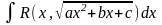 ,
где
,
где
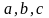 -некоторые
числа
-некоторые
числа
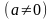 :
:
1)
если трёхчлен
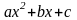 имеет вещественные корни
имеет вещественные корни
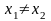 и
и
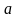 >0,
то
>0,
то
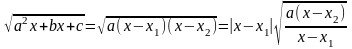 и
и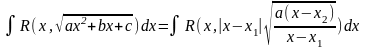 . Имеем предыдущий случай.
. Имеем предыдущий случай.
2)
если трёхчлен
не имеет вещественных корней и
>0,
то интеграл преобразуется подстановкой
Эйлера
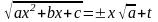 .
.
3) если трёхчлен не имеет вещественных корней, <0 и с>0,
то
применяют другую подстановку Эйлера
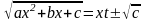 .
.
4)
выделим полный квадрат:
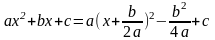 .
.
С
помощью подстановки
 интеграл сводится в зависимости от
коэффициентов
к одному из следующих интегралов:
интеграл сводится в зависимости от
коэффициентов
к одному из следующих интегралов:
 замена
замена

 замена
замена
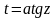 или
или
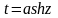
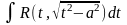 замена
замена
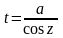 или
или
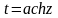
10.Интегрирование тригонометрических выражений
1.
Интегралы вида
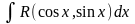 ,
где R-рациональная
функция, приводятся к интегралам от
рациональных функций с помощью так
называемой универсальной тригонометрической
подстановки
,
где R-рациональная
функция, приводятся к интегралам от
рациональных функций с помощью так
называемой универсальной тригонометрической
подстановки
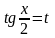 .
.
2.
Интегралы вида
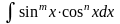 ,
где m
и n-положительные
целые
,
где m
и n-положительные
целые
чётные
числа, вычисляются с помощью формул:
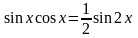
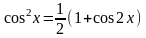
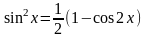
Если n-нечётное положительное число, то применяется
подстановка sinx = t,
если m-нечётное положительное число, то применяется
подстановка cosx = t.
В общем случае интегралы этого вида вычисляются с помощью рекуррентных формул, которые выводятся путём интегрирования по частям.
3.
Интегралы вида
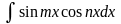
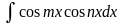 ,
,
 ,
,
где
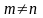 ,
вычисляются с помощью формул:
,
вычисляются с помощью формул:
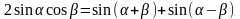
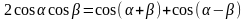
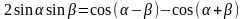
4.
Интегралы вида
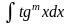 ,
,
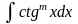 ,
где m
= 2,3,… вычисляются с помощью формул
,
где m
= 2,3,… вычисляются с помощью формул
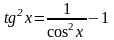
 .
.
11. Определение определенного интеграла и его св-ва
|
Пусть
на отрезке 1.С
помощью точек деления разобьем
отрезок
на n “малых”
отрезков где в каждом из малых
отрезков 4.Наибольшую
из длин малых отрезков обозначим λ и
назовем ее шагом
разбиения.
Пусть число отрезков разбиения
неограниченно растет . Если при
этом интегральная сумма Имеет место теорема существования определенного интеграла. Всякая
непрерывная на отрезке определенный
интеграл от неотрицательной непрерывной
функции численно равен площади
криволинейной трапеции, ограниченной
кривой |
основные свойства определенного интеграла
1.Если нижний и верхний пределы интегрирования равны (a=b), то интеграл равен нулю:
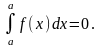 Это
свойство следует из определения
интеграла.
Это
свойство следует из определения
интеграла.
2.Если f(x)=1, то

Действительно, так как f(x)=1, то

3.При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:
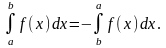
4.Постоянный множитель можно выносить за знак определенного интеграла:
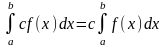
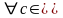 R.
R.
5.Определенный интеграл от алгебраической суммы конечного числа интегрируемых на [a; b] функций f1(x), f2(x), …, fn(x) равен алгебраической сумме определенных интегралов от слагаемых:

6.(аддитивность
определенного интеграла). Если существует
интегралы
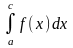 и
и
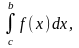 то существует
также интеграл
то существует
также интеграл
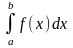 и для любых
чисел a,
b,
c;
и для любых
чисел a,
b,
c;

7.Если
f(x)
≥ 0
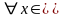 [a;
b],
то
[a;
b],
то
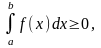 a<b.
a<b.
8.(определенность
определенного интеграла). Если
интегрируемые функции f(x)
и φ(x)
удовлетворяют неравенству f(x)
≥ φ(x)
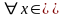 [a;
b],
то
[a;
b],
то
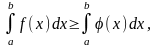 a>b.
a>b.
9.(об оценке определенного интеграла). Если m и М – соответственно наименьшее и наибольшее значения функции f(x), непрерывной на отрезке [a; b], то
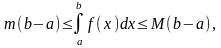 a<b.
a<b.
10.(теорема
о среднем). Если функция f(x)
непрерывна на отрезке [a;
b],
то существует такая точка
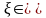 [a;
b],
что
[a;
b],
что
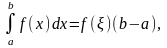 т.
е. определенный интеграл от переменной
функции равен произведению значения
подынтегральной функции в некоторой
промежуточной точке ξ отрезка
интегрирования [a;
b]
и длины b-a
этого отрезка.
т.
е. определенный интеграл от переменной
функции равен произведению значения
подынтегральной функции в некоторой
промежуточной точке ξ отрезка
интегрирования [a;
b]
и длины b-a
этого отрезка.
