5. Интегрирование по частям в не опред. Интеграле

Интегрированием по частям называется нахождение интеграла по формуле

,

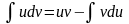где u(x) и v(x) - дифференцируемые функции.

Применение её целесообразно, когда интеграл в правой части формулы более прост для нахождения, нежели исходный. В некоторых случаях формулу необходимо применять несколько раз.

При этом за u(x) берётся такая функция, которая при дифференцировании упрощается, а за dv -та часть подынтегрального выражения, интеграл от которой известен или может быть найден. Так, например,

для интегралов вида , ,

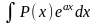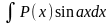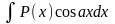
за u(x) следует принять многочлен P(x) .

Для интегралов вида , ,

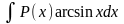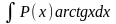
за u(x) принимаются функции lnx, arcsinx, arctgx, а за dv - выражение P(x)dx .

_Т.е.

Доказательство.

Пусть F₁(x) и F₂(x) соответственно некоторые первообразные для   и  .

Тогда по определению первообразной и правилу дифференцирования произведения двух функций  + = ,  .

Следовательно, по следствию из теоремы Лагранжа:

F₁(x) + F₂(x) =  + c, где c – некоторая константа, или F₁(x) =  - F₂(x).

Так как

 

из данного равенства следует, что 

Замечание: Формулу интегрирования по частям следует понимать так: множество функций {F₁(x) + C₁}, стоящих в левой части равенства, совпадает со множеством функций { -F₂(x) + c₃}, стоящих в правой части, где с₃ = с – с₂, а с₁ и с₂ – произвольные числа.

6. Интегрирование выраж содержащ квадратный трехчлен

1°. Интеграл вида

путем дополнения квадратного трехчлена до полного квадрата по формуле

сводится к одному из двух интегралов

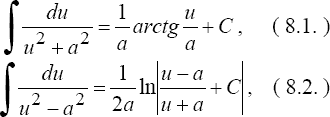
где u = х + k.

2°. Интеграл

сводится к интегралам вида (8.1) или (8.2) и интегралу

3°. Интеграл

сводится к одному из интегралов:

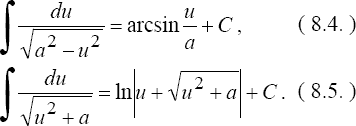
4°. Интеграл вида

сводится к одному из двух интегралов

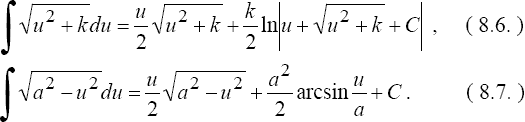
5°. Интеграл вида

сводится к разобранным выше интегралам.

7.Интегрирование простых правильных дробей

 Если P(z) и Q(z) – многочлены в комплексной области, то   - рациональная дробь. Она называется правильной, если степень P(z) меньше степени Q(z), и неправильной, если степень Р не меньше степени Q.

Любую неправильную дробь можно представить в виде:   

  ,где P(z) = Q(z) S(z) + R(z), a R(z) – многочлен, степень которого меньше степени Q(z).

Таким образом, интегрирование рациональных дробей сводится к интегрированию многочленов, то есть степенных функций, и правильных дробей, так как   является правильной дробью.

 Определение . Простейшими (или элементарными) дробями называются дроби следующих видов:

 1. ;

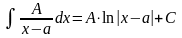
2. 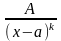, где к -целое число, больше единицы

3. 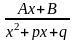, где 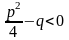, т.е. квадратный трёхчлен 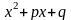не имеет действительных корней

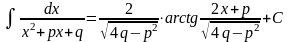
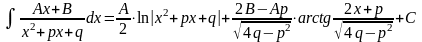
4.

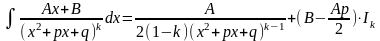
Вычисление интеграла 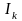производится по рекуррентной формуле :

8.Разложение рациональных дробей на простейшие, интегрирование рациональных функций.

Рациональной называется функция вида

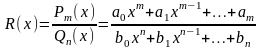
где m,n-целые, положительные числа. Если m<n,то R(x) называется правильной дробью, если m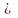 n ,то неправильной. Всякую неправильную дробь путём деления числителя на знаменатель можно представить в виде суммы некоторого многочлена и правильной дроби: 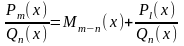, l<n.

Так как всякий многочлен легко интегрируется, то интегрирование рациональных функций сводится к интегрированию правильных дробей. Всякую правильную рациональную дробь можно разложить в сумму простейших рациональных дробей.

Теорема. Правильную рациональную дробь где можно единственным образом разложить на сумму простейших дробей:

 - (6)

(A₁, A₂, …, A_k, B₁, B₂, …, B₁, M₁, N₁, M₂, M₂, …, M_s, N_s – некоторые действительные числа).

Метод неопределенных коэффициентов. Суть метода неопределенных коэффициентов состоит в следующем. Пусть дано разложение правильной рациональной дроби  по формуле (6) на простейшие дроби с неопределенными коэффициентами. Приведем простейшие дроби к общему знаменателю Q_m(x)и приравняем многочлен, получившийся в числителе, многочлену P_n(x).

Метод частных значений. При нахождении неопределенных коэффициентов вместо того, чтобы сравнивать коэффициенты при одинаковых степенях х, можно дать переменной х несколько частных значений (по числу неопределенных коэффициентов) и получить таким образом систему уравнений относительно неопределенных коэффициентов. Особенно выгодно применять этот метод в случае, корни знаменателя рациональной дроби  просты и действительны. Тогда оказывается удобным последовательно полагать равным каждому из корней знаменателя.