
- •1. Первообразная и ее свойства
- •3. Таблица интегралов.
- •2.Неопределенный интеграл и его свойства
- •4.Замена переменной в неопределенном интеграле
- •5. Интегрирование по частям в не опред. Интеграле
- •6. Интегрирование выраж содержащ квадратный трехчлен
- •7.Интегрирование простых правильных дробей
- •9.Интегрирование некоторых классов иррац функций
- •10.Интегрирование тригонометрических выражений
- •11. Определение определенного интеграла и его св-ва
- •12. Интеграл с переменным верхним пределом;производная по верхнему пределу
- •13.Формула Ньютона-Лейбница
- •14.Замена переменной в определенном интеграле
- •15.Интегрирование по частям в определенном интеграле
- •16.Геометрические приложения определенного интеграла
- •17.Несобственные интегралы по бесконечному промежутку интегрир от непрерывных функций.
- •18.Несобственные интегралы по конечному промежутку интегрирования от неограниченных функций.
- •19. Диффер уравн: опред, решение уравн, задача Коши, общ и частн решения, геом смысл решений
- •20.Диффер уравнен первого порядка с разделенными и разделяющ переменными
- •21.Лин диффер уравнения 1го порядка(методы Бернулли и Лагранжа, их решения)
- •22.Лин диффер уравн 2го порядка с пост коэфф, структура их общ решения
- •23. Структура решения лин неоднор дифф уравн 2го порядка
- •24.Нахождение частных реш лин неоднор диффер уравн 2го порядка с пост коэфф по виду правой части
- •25. Числовой ряд и его сумма; сход и расход ряды
- •26. Геометрический и гармонический ряды
- •27. Необходимые условия сходимости ряда
- •28.Полож ряды; признаки сравнен их сходимости
- •29.Предельный признак Даламбера
- •30.Предельный признак Коши
- •31.Интегральный признак Маклорена-Коши
- •32.Знакоперемен ряды, абсол и условная сходимости
- •33.Теорема Коши об абсол сход знакоперем ряда
- •34.Признак Лейбница знакочеред рядов
- •35.Теорема Абеля сходимости степенного ряда
- •36.Радиус сходим степенного ряда и его нахождение
- •37. Понятие о рядах Тейлора и Маклорена
- •39.Разложение в ряд Маклорена ф-ции cos X, sin X
28.Полож ряды; признаки сравнен их сходимости
Определение
5.
Числовой ряд, все члены которого
неотрицательны, т.е. для любого

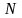 выполняется неравенство
выполняется неравенство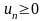 ,
(21) называют положительным
рядом . Такие
ряды точнее было бы называть рядами
с неотрицательными членами,
ряды с неположительными членами
(
,
(21) называют положительным
рядом . Такие
ряды точнее было бы называть рядами
с неотрицательными членами,
ряды с неположительными членами
(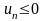 )
путём умножения на (-1) переходят в ряды
с неотрицательными членами и,
следовательно, можно будет сделать
выводы и об их сходимости.
)
путём умножения на (-1) переходят в ряды
с неотрицательными членами и,
следовательно, можно будет сделать
выводы и об их сходимости.
признаки сравнения.
Теорема 3. Пусть даны два положительных ряда
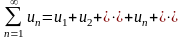 (22)
(22)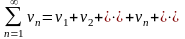 , (23)
, (23)
причём для всех выполняется неравенство
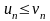 . (24)Тогда
из сходимости ряда (23) следует сходимость
ряда (22) (то есть, если сходится ряд с
большими членами, то сходится и ряд с
меньшими членами); из расходимости ряда
(22) следует расходимость ряда (23) (то
есть, если расходится ряд с меньшими
членами, то ряд с большими членами также
расходится).
Доказательство.
Обозначим частичные суммы рядов (22) и
(23), соответственно, через
. (24)Тогда
из сходимости ряда (23) следует сходимость
ряда (22) (то есть, если сходится ряд с
большими членами, то сходится и ряд с
меньшими членами); из расходимости ряда
(22) следует расходимость ряда (23) (то
есть, если расходится ряд с меньшими
членами, то ряд с большими членами также
расходится).
Доказательство.
Обозначим частичные суммы рядов (22) и
(23), соответственно, через
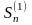 и
и
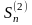 .
Из определения 2 n-й
частичной суммы ряда и неравенства
(24) следует неравенство
.
Из определения 2 n-й
частичной суммы ряда и неравенства
(24) следует неравенство
 .Пусть
ряд (23) сходится; тогда по теореме 2 его
частичные суммы ограничены сверху:
.Пусть
ряд (23) сходится; тогда по теореме 2 его
частичные суммы ограничены сверху:
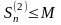 (необходимое условие). В силу предыдущего
неравенства получим, что и
(необходимое условие). В силу предыдущего
неравенства получим, что и
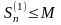 ,
откуда снова по теореме 2 (достаточное
условие) следует сходимость ряда (22).
,
откуда снова по теореме 2 (достаточное
условие) следует сходимость ряда (22).
Вторая часть утверждения этой теоремы есть следствие первой. В самом деле, если бы ряд (23) сходился, то согласно первому утверждению сходился бы и ряд (22), что противоречит предположению о его расходимости. Это же утверждение вытекает и из неравенства
Теорема
4. предельный
признак сравнения
Пусть ряд (22) – положительный, а ряд
(23) строго положительный
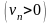 .
Если существует конечный, отличный от
нуля, предел отношения общих членов
этих рядов
.
Если существует конечный, отличный от
нуля, предел отношения общих членов
этих рядов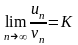
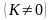 ,
(25) то оба ряда сходятся или расходятся
одновременно.
,
(25) то оба ряда сходятся или расходятся
одновременно.
Доказательство.
Если предел (25) существует, то по
определению предела числовой
последовательности для любого числа
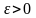 найдётся номер N
такой, что для всех
найдётся номер N
такой, что для всех
 будет выполняться неравенство
будет выполняться неравенство
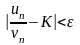 или
или
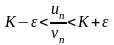 .Так
как по условию теоремы
.Так
как по условию теоремы
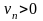 ,
то для всех
будет выполняться неравенство
,
то для всех
будет выполняться неравенство
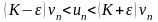 .
(26)
.
(26)
Поскольку
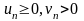 и предположено, что
и предположено, что
 ,
то
,
то
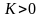 .
В силу произвольности числа
.
В силу произвольности числа
 его можно выбрать таким, чтобы число
его можно выбрать таким, чтобы число
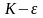 было положительным
было положительным
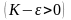 ;
для этого
,
может быть, придётся взять сколь угодно
малым. Неравенства (26) позволяют применять
теорему 3 (первый признак сравнения).
Именно, будем сравнивать положительные
ряды с членами
;
для этого
,
может быть, придётся взять сколь угодно
малым. Неравенства (26) позволяют применять
теорему 3 (первый признак сравнения).
Именно, будем сравнивать положительные
ряды с членами
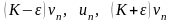 .Пусть
ряд с членами
сходится. Так как
.Пусть
ряд с членами
сходится. Так как
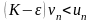 ,
то по первому признаку сравнения
(теорема 3) ряд с членами
,
то по первому признаку сравнения
(теорема 3) ряд с членами
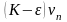 сходится, а тогда по свойству 2 сходится
и ряд с членами
сходится, а тогда по свойству 2 сходится
и ряд с членами
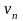 .Пусть
теперь сходится ряд с членами
.
Тогда по свойству 2 сходится ряд с
членами
.Пусть
теперь сходится ряд с членами
.
Тогда по свойству 2 сходится ряд с
членами
 .
Но так как согласно (26)
.
Но так как согласно (26)
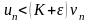 ,
то по теореме 3 сходится и ряд с членами
.
,
то по теореме 3 сходится и ряд с членами
.
Итак,
сходимость одного из рядов (22) и (23) при
 влечёт за собой сходимость другого
ряда (тем самым, если один из них
расходится, то расходится и другой).
Теорема доказана.
влечёт за собой сходимость другого
ряда (тем самым, если один из них
расходится, то расходится и другой).
Теорема доказана.
