8.2. Пример расчета маховика

Предположим, что уже построен график суммарно крутящего момента, например для дизеля 4Ч13/14.

Известно, что l = 0,09 м, F_{изб max} =12·10^-4 м² (12 см²), =180⁰.

Рассмотрим только 1/4 часть диаграммы суммарного крутящего момента от 0 до 180⁰. При повороте коленчатого вала от 180 до 720⁰ вид диаграммы повторяется, что указывает о правильности вычислений.

Определим по формуле (8.9) масштаб суммарной диаграммы крутящего момента

Н·м/ м².

По формуле (8.8) вычислим наибольшую избыточную работу

Н·м.

Задаваясь значением и определив

,

находим по формуле (8.2) момент инерции всех движущихся масс двигателя

кг·м².

Момент инерции маховика вычислим по формуле (8.11):

кг·м².

Принимая D_СР = 0,35 м, определим массу маховика

кг.

Принимая D_М = 0,4 м и материал маховика – сталь, по формуле (8.13) находим окружную скорость

м/с.

Окружная скорость не превышает допустимых значений [50 − 60] м/с.

Контрольные вопросы

1. Назначение маховика.

2. Что называют коэффициентом неравномерности хода?

3. Как определяют момент инерции маховика?

4. Как находится начальная фаза в цилиндре двигателя?

5. Как вычисляется наибольшая избыточная работа по диаграмме набегающего момента?

6. Как определяют масштаб площади суммарной диаграммы крутящего момента?

9. Расчет коленчатого вала двигателя на крутильные колебания

При эксплуатации двигателей внутреннего сгорания, даже полностью уравновешенных, на определенных скоростных режимах появляются вибрации и стуки, приводящие иногда к разрушению коленчатого вала. Причиной этого являются крутильные колебания вала, которые возникают вследствие недостаточной жесткости коленчатого вала под действием переменных по величине и направлению крутящих моментов двигателя [8, 31]. Крутильные колебания могут быть собственными и вынужденными.

Собственные колебания коленчатый вал совершает выведенный из состояния покоя под действием только момента сил упругости вала М_уп и момента сил инерции М_ин от вращающихся масс. Вынужденные колебания коленчатого вала возникают в процессе работы двигателя вследствие действия периодически изменяющихся крутящих моментов, которые вызывают упругие деформации скручивания коренных шеек.

При совпадении частот собственных крутильных колебаний с вынужденными колебаниями возникает резонанс. Создаются большие дополнительные напряжения кручения, приводящие к поломке вала.

9.1. Свободные крутильные колебания вала с одной массой

Рассмотрим колебания вала с маховиком. Вал жестко закреплен на свободном конце (рис. 9.1). Крутильная система имеет маховик массой m и моментом инерции J_м, вал длиной L с наружным диаметром d.

Колебание – движение, повторяемое во времени. Период – время в секундах одного полного колебания.

Приложим к маховику крутящий момент М_кр и закрутим вал на угол φ_с (например, 10⁰). Мгновенно устраним действие М_кр. Под действием момента сил упругости М_уп закрученный вал вернется в первоначальное положение. Далее, под действием момента сил инерции маховика М_ин , вал закрутится в противоположную сторону на угол φ_с. Предположим, что сопротивления колебаниям отсутствуют, а инерцией вала пренебрегаем. Тогда

, . (9.1)

Предположим, что одно полное колебание произошло за 2 с.

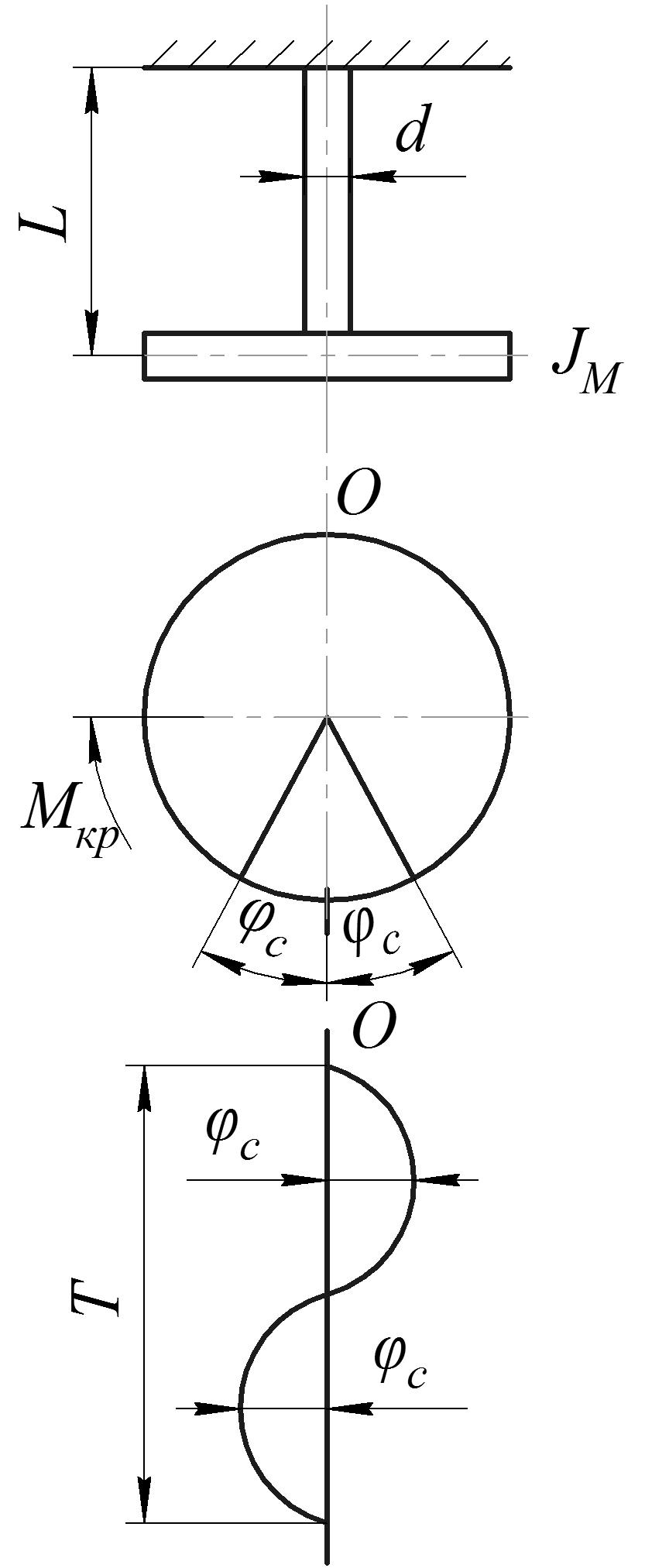
Рис. 9.1. Гармонические колебания системы

вала с одной массой

Период колебания Т равен 2 с. Амплитуда колебания равняется значению или максимальному углу поворота от своего нейтрального положения.

Частотой колебаний (кол/с) называют число колебаний за единицу времени

. (9.2)

Таким образом, в нашем примере .

Круговая частота (рад/с) – число полных колебаний, которые совершаются за 2π единиц времени.

. (9.3)

В нашем примере угловая скорость рад/с.

Из формулы (9.3) находим период .

При частоте вращения 1 об/с (за 1 с совершается оборот) система проходит 360⁰, или 6,28 радиан (2 рад). Один радиан равен 57,3⁰.

Момент касательных сил инерции определяется выражением

, (9.4)

где – угловое ускорение маховика 1/с² .

Момент упругости вала , согласно закону Гука, равен

, (9.5)

где G – модуль упругости материала при сдвиге (кручении), Н/м²; – момент инерции сечения вала диаметром d, в м⁴; – угол закручивания вала при деформации; L – длина вала, м.

Уравнение (9.5) можно представить в виде

, (9.6)

где – жесткость вала, представляющая собой крутящий момент, Н·м, необходимый для закручивания вала на 1⁰.

Используя выражение (9.1), запишем

. (9.7)

Разделим обе части выражения (9.7) на величину , получим

. (9.8)

Таким образом, мы получили линейное дифференциальное уравнение второго порядка с постоянными коэффициентами, алгоритм решения которого описан в п. 3.3.1 (гл. 3) настоящего пособия.

Введем обозначение

. (9.9)

Окончательно получим

, (9.10)

где − круговая, циклическая частота собственных крутильных колебаний, 1/с.

Уравнение (9.10) является дифференциальным уравнением свободных колебаний вала с одной массой. Найдем его решение (см. гл. 3). Так как соответствующее характеристическое уравнение имеет два комплексных сопряженных корня , следовательно, по табл. 3.1 (гл. 3) решение уравнения (9.10) будет иметь вид

. (9.11)

Постоянные величины и находят из начальных условий.

Начало движения – момент максимального угла закручивания вала при .

Из уравнения (9.11) получим

.

Для нахождения коэффициента воспользуемся вторым начальным условием, а именно . Для этого найдем выражения (9.11) функции .

.

Тогда .

Таким образом, подставив в выражение (9.11) значения , получим

. (9.12)

Уравнение (9.12) выражает гармоническое колебательное движение, в котором является амплитудой или максимальным углом поворота маховика от своего нейтрального положения.