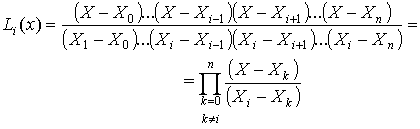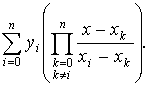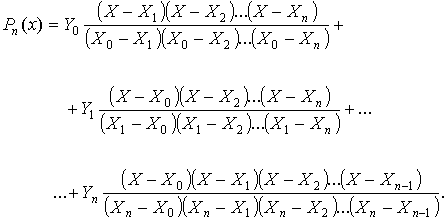2.2. Интерполяционный многочлен Лагранжа

Пусть функция f(x) задана таблично. Это могут быть, например, значения концентраций продуктов реакции в зависимости от температуры, полученные экспериментально.

x	x0      x1 . . . . xn
f (x)	f 0     f 1 . . . . fn

Значения x₀,x₁,..., x_n называются узлами таблицы. Считаем, что узлы в общем случае не являются равноотстоящими (шаг таблицы неравномерный).

Построим интерполяционный многочлен на отрезке [x₀,x_n]. Запишем искомый многочлен в виде

Pm(x) = a0 + a1x + a2x2 +. . . + amxm .

(5.5)

Геометрически задача интерполирования сводится к построению кривой через заданные точки.

Аналитически задача сводится к решению системы уравнений

(5.6)

Для определения коэффициентов многочлена (5.5) необходимо располагать n+1 узловой точкой.

Чтобы система уравнений имела единственное решение, необходимо, чтобы количество неизвестных (коэффициенты полинома а_j) - m+1 - равнялось количеству уравнений n+1или m=n.

Пусть в n+1-ой точках x₀, x₁,..., x_n определены значения y₀, y₁,..., y_n. Требуется построить многочлен P_n(x), принимающий в узловых точках заданные значения   y_i, т.е. такой, что

P_n(x_i) = y_i, i= 0,1, ...,n.

Лагранж предложил следующую форму интерполяционного полинома

,

(5.7)

где L_i(x) - множитель Лагранжа, имеющий вид:

(5.8)

Следовательно , формулу Лагранжа можно представить в виде:

Pn (x)=

(5.9)

Числитель и знаменатель не должны включать в себя значения x =x_i, так как результат будет равен нулю. В развернутом виде формулу Лагранжа можно записать:

(5.10)

Блок - схема метода Лагранжа приведена на рис.5.2.

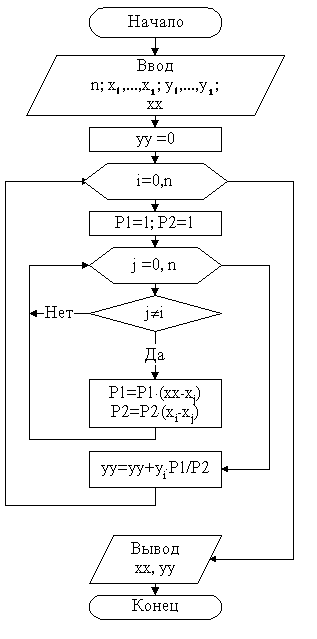Рис. 5.2. Блок-схема метода Лагранжа

Пример 5.1. Для функции y=sin x построить интерполяционный полином Лагранжа, выбрав узлы: x₀, x₁, x₂.

X	0
Y	0		1

Применяя формулу (5.10), получим:

.

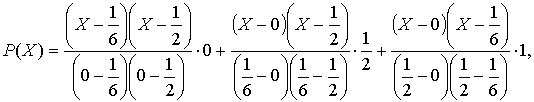
Пример 5.2. Дана таблица значений теплоёмкости вещества в зависимости от температуры C_p = f (T).

x (T)	300	400	500	600
y (Cp)	52.89	65.61	78.07	99.24

Вычислить значение теплоёмкости в точке Т=450 К.

Для решения воспользуемся формулой (5.10).

Значение теплоемкости при температуре 450 К получим:

.

2.3. Интерполяционные многочлены Ньютона

Конечные разности.

Пусть задана функция y = f (x) на отрезке [x₀,x_n], который разбит на n одинаковых отрезков (случай равноотстоящих значений аргумента). x=h=const. Для каждого узла x₀, x₁=x₀+h, ..., x_n=x₀+n^.h определены значения функции в виде:

f (x0)=y0,   f (x1)=y1, ..., f(xn)=yn.

(5.11)

Введем понятие конечных разностей.

Конечные разности первого порядка

y₀ = y₁ - y₀;

y₁ = y₂ - y₁;

.      .         .       .       .

y_n-1 = y_n - y_n-1.

Конечные разности второго порядка

2y₀ = y₁ - y₀;

2y₁ = y₂ - y₁;

.     .         .        .          .          .

2y_n-2 = y_n-1 - y_n-2.

Аналогично определяются конечные разности высших порядков:

^ky₀ = ^k-1y₁ - ^k-1y₀;

^ky₁ = ^k-1y₂ - ^k-1y₁;

.             .          .          .          .          .

^ky_i = ^k-1y_i+1 - ^k-1y_i , i = 0,1,...,n-k.

Конечные разности функций удобно располагать в таблицах, которые могут быть диагональными (табл.5.1) или горизонтальными (табл.5.2) таблицами разностей.

Таблица 5.1

xi	yi	yi	2yi	3yi	4yi	5yi
x0	y0
		y0
x1	y1		2y0
		y1		3y0
x2	y2		2y1		4y0
		y2		3y1		5y0
x3	y3		2y2		4y1
		y3		3y2
x4	y4		2y3
		y4
x5	y5

Диагональная таблица

Таблица 5.2
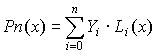