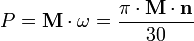- •Модели в механике. Система отсчета. Траектория, длина пути, вектор перемещения. Мгновенная скорость, мгновенное ускорение.
- •Криволинейное движение материальной точки. Вывод формул тангенциального и нормального ускорений. Простейшие виды движения материальной точки.
- •Вращательное движение. Угол поворота. Угловая скорость. Угловое ускорение. Связь между угловыми и линейными характеристиками движения.
- •Динамика материальной точки. Масса. Сила. Законы Ньютона. Инерциальные системы отсчета. Импульс силы.
- •Механическая система. Внутренние и внешние силы. Центр масс.
- •Понятие энергии и работы. Работа переменной силы. Консервативные и диссипативные силы. Мощность.
- •7. Потенциальная энергия. Потенциальные поля. Потенциальная энергия гравитационного взаимодействия и упругой деформации.
- •Работа упругой силы (потенциальная энергия упруго деформированного тела)
- •8. Кинетическая энергия. Полная механическая энергия системы.
- •Вращательное движение твердого тела. Динамические .Характеристики {момент силы, момент инерции). Теорема Штейнера.
- •1.Момент силы, действующей на материальную точку, относительно оси вращения.
- •2. Момент импульса.
- •3. Момент инерции материальной точки относительно оси вращения
- •4.Теорема Штейнера.
- •Кинетическая энергия вращающегося тела. Основное уравнение динамики вращательного движения.
- •Основные величины поступательного движения и их аналоги во вращательном движении. Аналоги трех законов Ньютона для вращательного движения твердого тела
- •Закон всемирного тяготения. Сила тяжести. Вес. Невесомость.
- •Поле тяготения. Напряженность и потенциал поля.
- •Неинерциальные системы отсчета. Силы инерции при ускоренном поступательном движении системы отсчета. Примеры
- •Неинерциальные системы отсчета. Силы инерции, действующие из тело, покоящееся во вращающейся системе отсчета.
- •Неинерциальные системы отсчета. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета.
- •Уравнение движения тела переменной массы.
- •Силы трения. Виды трения. Коэффициент трения.
- •Деформация твердого тела. Деформация растяжения (сжатия). Закон Гука. Деформация сдвига.
- •Закон сохранения импульса. Абсолютно неупругий удар.
- •21. Закон сохранения механической энергии. Абсолютно упругий удар.
- •22. Момент импульса твердого тела. Закон сохранения момента импульса.
- •Преобразования Галилея. Принцип относительности в классической механике.
- •Специальная теория относительности. Постулаты Эйнштейна. Преобразования Лоренца.
- •Вид преобразований при коллинеарных (параллельных) пространственных осях
- •Важнейшие следствия из преобразований Лоренца: одновременность событий, длительность событий, длина тел в различных системах отсчета.
- •Специальная теория относительности. Закон взаимодействия массы и энергии.
- •Гармонические колебательные движения. Свободные колебания. Дифференциальное уравнение свободных незатухающих колебаний.
- •1.1. Свободные незатухающие колебания пружинного маятника
- •Пружинный, физический, математический маятники. Маятник Максвелла.
- •Дифференциальное уравнение свободных затухающих колебаний и его решение. Декремент затухания, логарифмический декремент затухания, добротность контура.
- •30. Дифференциальное уравнение вынужденных колебаний и его решение. Явление механического резонанса. Резонансные кривые.
- •31. Волновые процессы. Уравнение бегущей волны. Фазовая скорость. Понятие дисперсии. Волновое уравнение. Стоячие волны.
- •32. Звуковые волны. Эффект Доплера в акустике.
- •33. Статистический и термодинамический методы исследования. Параметры состояния системы. Равновесные состояния. Равновесные процессы.
- •Основное уравнение молекулярно-кинетической теории идеальных газов. Связь между температурой и средней кинетической энергией поступательного движения молекулы газа.
- •Распределение по проекции скорости
- •Распределение по модулю скоростей
- •Внутренняя энергия идеального газа. Понятие числа степеней свободы молекулы. Закон о равномерном распределении энергии по степеням свободы.
- •Понятие эффективного диаметра молекулы. Среднее число столкновений одной молекулы в единицу времени. Средняя длина свободного пробега молекулы и ее зависимость от давления и температуры.
- •Первый закон термодинамики. Внутренняя энергия системы. Работа, совершаемая газом.
- •Применение первого закона термодинамики к изобарическому и изотермическому процессам.
- •41. Применение первого закона термодинамики к изохорическому и адиабатическому процессам.
- •42. Теплоемкость (удельная, молярная). Уравнение Майера. Связь теплоемкости с числом степеней свободы молекулы.
- •43. Политропические процессы в идеальном газе. Уравнение политропы. Изопроцессы, как частные случаи политропического процесса. Теплоемкость при политропическом процессе.
- •Круговые процессы (циклы). Обратимые и необратимые процессы. Примеры. Тепловая машина и ее кпд. Цикл Карно и его кпд. . .
- •Второй закон термодинамики и его различные формулировки.
- •Энтропия. Основные свойства энтропии (формулировка второго закона термодинамики). Статистический смысл энтропии. Формула Больпмана.
- •47. Явления переноса. Теплопроводность, диффузия, внутреннее трение в газах. Уравнения, описывающие эти явления. Коэффициенты переноса.
- •Реальные газы. Силы межмолекулярного взаимодействия
- •Реальные газы. Уравнение Ван-дер-Ваальса. Смысл поправок в уравнении.
- •Изотермы реального газа. Критические параметры реального газа. Экспериментальные изотермы реального газа.
- •Внутренняя энергия реального газа. Эффект Джоуля-Томсона.
- •Фазовые превращения "твердых тел. Плавление и кристаллизация.
- •Вязкость (внутреннее трение). Методы определения вязкости.
Понятие энергии и работы. Работа переменной силы. Консервативные и диссипативные силы. Мощность.
Р абота
постоянной силы ее свойства.
Для характеристики эффективности
силового воздействия на тело используется
величина, называемая механической
работой. Пусть под действием постоянной
силы F
тело сместилось из положения 1 в положение
2 вдоль прямой линии (см. рис. 8.1).
абота
постоянной силы ее свойства.
Для характеристики эффективности
силового воздействия на тело используется
величина, называемая механической
работой. Пусть под действием постоянной
силы F
тело сместилось из положения 1 в положение
2 вдоль прямой линии (см. рис. 8.1).
Смещение тела охарактеризуем вектором перемещения S. Работой силы F на перемещении S называется скалярная величина, определяемая равенством: A = |F|·|S|·cosa = (F·S) (8.1)
Работа постоянной силы равняется скалярному произведению силы на перемещение.
Единица измерения работы - Джоуль. 1 Дж = 1 Н·м. Из уравнения (8.1) следует, что работу совершает только тангенциальная составляющая силы A = Ft·S.
Свойства работы:
|
перпендикулярная перемещению составляющая силы работы не производит; |
|
работа результирующей силы равна сумме работ составляющих сил: A = Ft·S = SFti·S = SAi; |
|
работа на перемещении S равна сумме работ на отдельных участках этого перемещения, т.е. работа является аддитивной величиной: A = Ft·SDSi = SAi. (8.2) |
Работа переменной силы. В общем случае криволинейного движения величина работы рассчитывается посредством интегрирования. Для этого все перемещение мысленно разобьем на отдельные элементарные участки DS такой малой длины, что их можно считать прямолинейными, а действующую на этих участках силу - постоянной (см. рис. 8.2).
 Рис.
8.2. Перемещение тела по кривой под
действием силы F.
Рис.
8.2. Перемещение тела по кривой под
действием силы F.
Работу
при перемещении частицы из начального
положения в конечное рассчитаем согласно
выражению (8.2), где Ai
- работа силы на каждом участке. Предел
суммы работ на отдельных участках
траектории 1-2 при DS
стремящемся к нулю является определенным
интегралом и представляет собой искомую
величину работы:
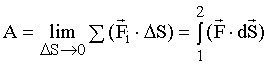 (8.3)
(8.3)
Работу силы F при конечном перемещении DS = S2 - S1 можно найти графически. Как следует из определения работы, ее значение в случае постоянной силы равно площади закрашенного прямоугольника (см. рис. 8.3). Аналогично вычисляется работа переменной силы. На рис. 8.4 поясняется, чему равна работа переменной силы F, направленной вдоль оси OX, при конечном перемещении тела вдоль этой оси. Кроме контактных взаимодействий, возникающих между соприкасающимися телами, наблюдаются взаимодействия между телами, удаленными друг от друга. Такие взаимодействия осуществляются посредством физических полей. Стационарное поле, в котором работа, совершаемая над частицей силами поля, зависит лишь от начального и конечного положений частицы и не зависит от пути, по которому она двигалась, называют потенциальным. Силы, действующие в потенциальных полях, называют консервативными. Работа консервативной силы на замкнутом пути равна нулю. Примеры консервативных сил – сила тяжести, сила упругости.
Если
же работа, совершаемая силой, зависит
от траектории перемещения тела из одной
точки в другую, то такая сила называется
неконсервативной (или диссипативной).
Типичные неконсервативные силы – силы
трения.
Мо́щность —
физическая
величина,
равная отношению работы,
выполняемой за некоторый промежуток
времени, к этому промежутку времени.
Различают среднюю мощность за промежуток
времени
![]() :
:
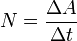
и
мгновенную мощность в данный момент
времени:
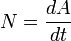
Так как работа является мерой изменения энергии, мощность можно определить также как скорость изменения энергии системы.
Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
|
|
F —
сила, v —
скорость,
![]() —
угол между вектором скорости и силы.
—
угол между вектором скорости и силы.
Частный случай мощности при вращательном движении:
|
|
M —
момент силы,
![]() —
угловая скорость,
—
угловая скорость,
![]() —
число пи,
n —
частота вращения (число оборотов в
минуту, об/мин).
—
число пи,
n —
частота вращения (число оборотов в
минуту, об/мин).