42. Теплоемкость (удельная, молярная). Уравнение Майера. Связь теплоемкости с числом степеней свободы молекулы.

УРАВНЕНИЕ МАЙЕРА - ур-ние, устанавливающее связь между теплоёмкостями при пост, давлении Cp и пост, объёме С_V 1 кмоля идеального газа: где R - газовая постоянная . Для произвольной массы т (кг) вещества в состоянии идеального газа уравнение Майера записывается в виде: , где - молекулярная масса газа. M. у. можно получить из общего соотношения ,если учесть, что для идеального газа справедливо Клапейрона уравнение.

Каждое независимое движение называется степенью свободы. Таким образом, одноатомная молекула имеет 3 поступательные степени свободы, «жесткая» двухатомная молекула имеет 5 степеней (3 поступательные и 2 вращательные), а многоатомная молекула – 6 степеней свободы (3 поступательные и 3 вращательные). В классической статистической физике доказывается так называемая теорема о равномерном распределении энергии по степеням свободы: Если система молекул находится в тепловом равновесии при температуре T, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна Из этой теоремы следует, что молярные теплоемкости газа Cp и CV и их отношение γ могут быть записаны в виде

где i – число степеней свободы газа.  Для газа, состоящего из одноатомных молекул (i = 3)

  Для газа, состоящего из двухатомных молекул (i = 5)

  Для газа, состоящего из многоатомных молекул (i = 6)

Теплоёмкость тела (обозначается C) — физическая величина, определяющая отношение бесконечно малого количества теплоты ΔQ, полученного телом, к соответствующему приращению его температуры ΔT: Единица измерения теплоёмкости в системе СИ — Дж/К. Удельная теплоемкость вещества — величина, равная количеству теплоты, необходи­мому для нагревания 1 кг вещества на 1 К: Единица удельной теплоемкости — джоуль на килограмм-кельвин (Дж/(кг × К)). Молярная теплоемкость—величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К:      где n=m/М—количество вещества. Единица молярной теплоемкости — джоуль на моль-кельвин (Дж/(моль × К)). Удельная теплоемкость с связана с молярной С_m, соотношением      где М — молярная масса вещества. Различают теплоемкости при постоянном объеме и постоянном давлении, если в процессе нагревания вещества его объем или давление поддерживается постоянным.

43. Политропические процессы в идеальном газе. Уравнение политропы. Изопроцессы, как частные случаи политропического процесса. Теплоемкость при политропическом процессе.

Политропный процесс, политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной.

В соответствии с сущностью понятия теплоёмкости , предельными частными явлениями политропного процесса являются изотермический процесс ( ) и адиабатный процесс ( ).

В случае идеального газа, изобарный процесс и изохорный процесс также являются политропными ^?.

Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Для идеального газа уравнение политропы может быть записано в виде:

где р — давление, V — объем газа, n — «показатель политропы».

. Здесь  — теплоёмкость газа в данном процессе, и  — теплоемкости того же газа, соответственно, при постоянном давлении и объеме.

В зависимости от вида процесса, можно определить значение n:

• Изотермический процесс: 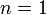, так как 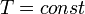, значит, по закону Бойля — Мариотта 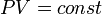, и уравнение политропы вынуждено выглядеть так: .

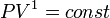• Изобарный процесс: 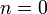, так как 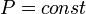, и уравнение политропы вынуждено выглядеть так: .

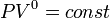• Адиабатный процесс: 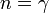(здесь 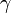— показатель адиабаты), это следует из уравнения Пуассона.

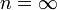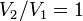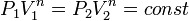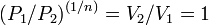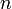• Изохорный процесс: , так как , и в процессе , а из уравнения политропы следует, что , то есть, что , то есть , а это возможно, только если является бесконечным.