
- •Модели в механике. Система отсчета. Траектория, длина пути, вектор перемещения. Мгновенная скорость, мгновенное ускорение.
- •Криволинейное движение материальной точки. Вывод формул тангенциального и нормального ускорений. Простейшие виды движения материальной точки.
- •Вращательное движение. Угол поворота. Угловая скорость. Угловое ускорение. Связь между угловыми и линейными характеристиками движения.
- •Динамика материальной точки. Масса. Сила. Законы Ньютона. Инерциальные системы отсчета. Импульс силы.
- •Механическая система. Внутренние и внешние силы. Центр масс.
- •Понятие энергии и работы. Работа переменной силы. Консервативные и диссипативные силы. Мощность.
- •7. Потенциальная энергия. Потенциальные поля. Потенциальная энергия гравитационного взаимодействия и упругой деформации.
- •Работа упругой силы (потенциальная энергия упруго деформированного тела)
- •8. Кинетическая энергия. Полная механическая энергия системы.
- •Вращательное движение твердого тела. Динамические .Характеристики {момент силы, момент инерции). Теорема Штейнера.
- •1.Момент силы, действующей на материальную точку, относительно оси вращения.
- •2. Момент импульса.
- •3. Момент инерции материальной точки относительно оси вращения
- •4.Теорема Штейнера.
- •Кинетическая энергия вращающегося тела. Основное уравнение динамики вращательного движения.
- •Основные величины поступательного движения и их аналоги во вращательном движении. Аналоги трех законов Ньютона для вращательного движения твердого тела
- •Закон всемирного тяготения. Сила тяжести. Вес. Невесомость.
- •Поле тяготения. Напряженность и потенциал поля.
- •Неинерциальные системы отсчета. Силы инерции при ускоренном поступательном движении системы отсчета. Примеры
- •Неинерциальные системы отсчета. Силы инерции, действующие из тело, покоящееся во вращающейся системе отсчета.
- •Неинерциальные системы отсчета. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета.
- •Уравнение движения тела переменной массы.
- •Силы трения. Виды трения. Коэффициент трения.
- •Деформация твердого тела. Деформация растяжения (сжатия). Закон Гука. Деформация сдвига.
- •Закон сохранения импульса. Абсолютно неупругий удар.
- •21. Закон сохранения механической энергии. Абсолютно упругий удар.
- •22. Момент импульса твердого тела. Закон сохранения момента импульса.
- •Преобразования Галилея. Принцип относительности в классической механике.
- •Специальная теория относительности. Постулаты Эйнштейна. Преобразования Лоренца.
- •Вид преобразований при коллинеарных (параллельных) пространственных осях
- •Важнейшие следствия из преобразований Лоренца: одновременность событий, длительность событий, длина тел в различных системах отсчета.
- •Специальная теория относительности. Закон взаимодействия массы и энергии.
- •Гармонические колебательные движения. Свободные колебания. Дифференциальное уравнение свободных незатухающих колебаний.
- •1.1. Свободные незатухающие колебания пружинного маятника
- •Пружинный, физический, математический маятники. Маятник Максвелла.
- •Дифференциальное уравнение свободных затухающих колебаний и его решение. Декремент затухания, логарифмический декремент затухания, добротность контура.
- •30. Дифференциальное уравнение вынужденных колебаний и его решение. Явление механического резонанса. Резонансные кривые.
- •31. Волновые процессы. Уравнение бегущей волны. Фазовая скорость. Понятие дисперсии. Волновое уравнение. Стоячие волны.
- •32. Звуковые волны. Эффект Доплера в акустике.
- •33. Статистический и термодинамический методы исследования. Параметры состояния системы. Равновесные состояния. Равновесные процессы.
- •Основное уравнение молекулярно-кинетической теории идеальных газов. Связь между температурой и средней кинетической энергией поступательного движения молекулы газа.
- •Распределение по проекции скорости
- •Распределение по модулю скоростей
- •Внутренняя энергия идеального газа. Понятие числа степеней свободы молекулы. Закон о равномерном распределении энергии по степеням свободы.
- •Понятие эффективного диаметра молекулы. Среднее число столкновений одной молекулы в единицу времени. Средняя длина свободного пробега молекулы и ее зависимость от давления и температуры.
- •Первый закон термодинамики. Внутренняя энергия системы. Работа, совершаемая газом.
- •Применение первого закона термодинамики к изобарическому и изотермическому процессам.
- •41. Применение первого закона термодинамики к изохорическому и адиабатическому процессам.
- •42. Теплоемкость (удельная, молярная). Уравнение Майера. Связь теплоемкости с числом степеней свободы молекулы.
- •43. Политропические процессы в идеальном газе. Уравнение политропы. Изопроцессы, как частные случаи политропического процесса. Теплоемкость при политропическом процессе.
- •Круговые процессы (циклы). Обратимые и необратимые процессы. Примеры. Тепловая машина и ее кпд. Цикл Карно и его кпд. . .
- •Второй закон термодинамики и его различные формулировки.
- •Энтропия. Основные свойства энтропии (формулировка второго закона термодинамики). Статистический смысл энтропии. Формула Больпмана.
- •47. Явления переноса. Теплопроводность, диффузия, внутреннее трение в газах. Уравнения, описывающие эти явления. Коэффициенты переноса.
- •Реальные газы. Силы межмолекулярного взаимодействия
- •Реальные газы. Уравнение Ван-дер-Ваальса. Смысл поправок в уравнении.
- •Изотермы реального газа. Критические параметры реального газа. Экспериментальные изотермы реального газа.
- •Внутренняя энергия реального газа. Эффект Джоуля-Томсона.
- •Фазовые превращения "твердых тел. Плавление и кристаллизация.
- •Вязкость (внутреннее трение). Методы определения вязкости.
Деформация твердого тела. Деформация растяжения (сжатия). Закон Гука. Деформация сдвига.
Сила упругости возникает в результате деформации тела и направлена в сторону, противоположную деформации.
При малых по сравнению с размерами тел деформациях сила упругости прямо пропорциональна величине абсолютной деформации тела. В проекции на направление деформирования сила упругости равна
 ,
где
x
– абсолютная деформация, k
– коэффициент жесткости.
,
где
x
– абсолютная деформация, k
– коэффициент жесткости.
Этот закон был установлен экспериментально английским ученым Робертом Гуком и называется законом Гука
Сила упругости, возникающая при деформации тела, пропорциональна удлинению тела и направлена в сторону, противоположную направлению перемещений частиц тела при деформации.
Коэффициент пропорциональности в законе Гука называется жесткостью тела. Он зависит от формы и размеров тела и от материала, из которого оно изготовлено (уменьшается с увеличением длины и с уменьшением площади поперечного сечения ).
В
Си жесткость выражается в ньютонах
на метр:
 .
.
Упругая сила стремится восстановить форму тела, подвергнутого деформации, и приложена к телу, которое эту деформацию вызывает.
Природа силы упругости электромагнитная, т.к. сила упругости возникает в результате стремления электромагнитных сил, действующих между атомами вещества, вернуть атомы вещества в исходное положение при изменении их взаимного положения в результате деформации.
Упругая реакция опоры, нити, подвеса – пассивная сила, действующая всегда перпендикулярно поверхности опоры.
Деформация сдвига (см. рис. 228, в) возникает в тех случаях, когда внешние силы, действующие на брус, расположены в параллельных плоскостях на очень малом расстоянии друг от друга и направлены в противоположные стороны. Характерным примером для сдвига является резание материалов ножницами, при этом происходит разрушение, называемое срезом. При деформациях сдвига возникают касательные напряжения, определяемые формулой τср=Q:F.
При сдвиге справедлив закон Гука, который определяется таким образом:
τ=Gγ, где γ - относительный сдвиг, a G - величина модуля упругости при сдвиге.
Порядок расчета на прочность при сдвиге такой же, как и при расчетах при растяжении (сжатии).
Для определения [τср] пользуются найденными из опыта закономерностями: для хрупких материалов [τср]≈[σр]; для пластических материалов [τср]≈0,5[σр].
Закон сохранения импульса. Абсолютно неупругий удар.
Импульс
тела - это произведение массы тела на
его скорость (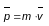 ).
Импульс тела - величина векторная.
Предположим, что взаимодействуют друг
с другом два тела (тележки) (см. рис.) с
массами m1
и m2,
движущиеся относительно выбранной
системы отсчета со скоростями
).
Импульс тела - величина векторная.
Предположим, что взаимодействуют друг
с другом два тела (тележки) (см. рис.) с
массами m1
и m2,
движущиеся относительно выбранной
системы отсчета со скоростями
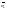 и
и
 .
На тела при их взаимодействии
действовали соответственно силы
.
На тела при их взаимодействии
действовали соответственно силы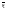 и
и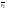 ,
и после взаимодействия они стали
двигаться со скоростями
,
и после взаимодействия они стали
двигаться со скоростями
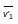 и
и
 .
Тогда
.
Тогда
 ,
,
 ,
t
- время взаимодействия. Согласно
третьему закону Ньютона
,
t
- время взаимодействия. Согласно
третьему закону Ньютона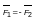 ,
следовательно,
,
следовательно,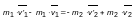 или
или
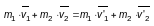 .
В левой части равенства - сумма импульсов
обоих тел (тележек) до взаимодействия,
в правой - сумма импульсов тех же тел
после взаимодействия. Импульс каждой
тележки изменился, сумма же осталась
неизменной. Это справедливо для
замкнутых систем, к которым относят
группы тел, которые не взаимодействуют
с другими телами, не входящими в эту
группу. Отсюда вывод, т. е. закон
сохранения импульса: Геометрическая
сумма импульсов тел, составляющих
замкнутую систему, остается постоянной
при любых взаимодействиях тел этой
системы между собой. Примером
проявления закона сохранения импульса
является реактивное движение. Оно
наблюдается в природе (движение
осьминога) и очень широко в технике
(водометный катер, огнестрельное оружие,
движение ракет и маневрирование
космических кораблей)
.
В левой части равенства - сумма импульсов
обоих тел (тележек) до взаимодействия,
в правой - сумма импульсов тех же тел
после взаимодействия. Импульс каждой
тележки изменился, сумма же осталась
неизменной. Это справедливо для
замкнутых систем, к которым относят
группы тел, которые не взаимодействуют
с другими телами, не входящими в эту
группу. Отсюда вывод, т. е. закон
сохранения импульса: Геометрическая
сумма импульсов тел, составляющих
замкнутую систему, остается постоянной
при любых взаимодействиях тел этой
системы между собой. Примером
проявления закона сохранения импульса
является реактивное движение. Оно
наблюдается в природе (движение
осьминога) и очень широко в технике
(водометный катер, огнестрельное оружие,
движение ракет и маневрирование
космических кораблей)
Выясним,
как изменяются импульсы двух тел при
их взаимодействии. Обозначим скорости
тел массами m1
и m2
до взаимодействия через
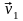 и
и
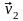 ,
а после взаимодействия – через
,
а после взаимодействия – через
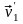 и
и
 .
.
По 3-му закону Ньютона силы, действующие на тела при их взаимодействии, равны по модулю и противоположны по направлению; поэтому из можно обозначить F и –F. Тогда:
 .
.
Таким образом, векторная сумма импульсов двух тел до взаимодействия равна векторной сумме их импульсов после взаимодействия.
Эксперименты показывают, что в любой системе взаимодействующих между собой тел при отсутствии действия сил со стороны других тел, не входящих в систему, – в замкнутой системе – геометрическая сумма импульсов тел остается постоянной. Импульс замкнутой системы тел есть величина постоянная – закон сохранения импульса (з.с.и.).
А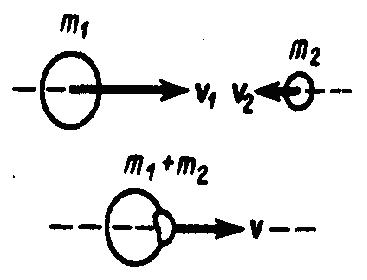 бсолютно
неупругий удар
- соударение двух тел, в результате
которого тела соединяются, двигаясь
дальше как единое целое. Абсолютно
неупругий удар можно продемонстрировать
с помощью шаров из пластилина (глины),
которые движутся навстречу друг другу
(рис. 5).
бсолютно
неупругий удар
- соударение двух тел, в результате
которого тела соединяются, двигаясь
дальше как единое целое. Абсолютно
неупругий удар можно продемонстрировать
с помощью шаров из пластилина (глины),
которые движутся навстречу друг другу
(рис. 5).
Рис.5
Если массы шаров m1 и m2, их скорости до удара ν1 и ν2, то, используя закон сохранения импульса
![]()
где v - скорость движения шаров после удара. Тогда
![]() (15.10)
В случае движения шаров навстречу
друг другу они вместе будут продолжать
движение в ту сторону, в которую двигался
шар с большим импульсом. В частном
случае, если массы шаров равны (m1=m2),
то
(15.10)
В случае движения шаров навстречу
друг другу они вместе будут продолжать
движение в ту сторону, в которую двигался
шар с большим импульсом. В частном
случае, если массы шаров равны (m1=m2),
то
![]()
