
- •28. Почленное интегрирование и дифференцирование функциональных рядов.
- •29. Степенной ряд и его область сходимости.
- •30. Аналитические функции. Ряд Тейлора.
- •31. Разложение в ряды Маклорена основных элементарных функций.
- •32.Тригонометрическая система функций.
- •33.Тригонометрические ряды Фурье.
- •34.Разложение в ряд Фурье четных и нечетных функций
- •35.Ряд Фурье для функций, заданных на отрезке [-l;l].
- •36. Интеграл Фурье.
- •37. Косинус- и синус-преобразование Фурье.
- •38.Дифференциальные уравнения. Основные определения
- •39.Дифференциальные уравнения с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка.
- •40.Линейные дифференциальные уравнения. Уравнения Бернулли.
- •41.Дифференциальные уравнения в полных дифференциалах.
- •42.Дифференциальные уравнения высших порядков. Уравнения, допускающие понижение порядка.
- •43) Линейные однородные дифференциальные уравнения высших порядков с постоянными коэффициентами.
- •51) Ряд Тейлора. Разложение некоторых элементарных функций в ряд Тейлора.
- •54.Изолированные особые точки аналитических функций: устранимые особые точки; полюсы и их связь с нулями; существенно особые точки.
- •55. Вычеты аналитических функций. Основная теорема о вычетах.
- •56. Приложения вычетов к вычислению определённых интегралов.
28. Почленное интегрирование и дифференцирование функциональных рядов.
u1(x) + u2(x) +…+ un(x) +… , где un(x) = f (x,n), называется функциональным рядом.
Теорема о почленном интегрировании.
 функция
функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]()
 на
на
Тогда
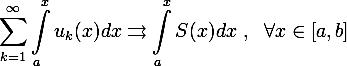
Теорема о почленном дифференцировании.
функция непрерывно дифференцируема на отрезке
 сходится
сходится
![]() равномерно
сходится на отрезке
.
равномерно
сходится на отрезке
.
Тогда
 —
непрерывно дифференцируема на
,
—
непрерывно дифференцируема на
, на
.
на
.
29. Степенной ряд и его область сходимости.
Степенным рядом называется функциональный ряд вида

где a0, a1, a2, …,an,…, а также x0 – постоянные числа. Точку x0 называют центром степенного ряда.
Сначала рассмотрим степенные ряды с центром 0, т.е. ряды вида
 (1.2)
(1.2)
Такой ряд всегда сходится при x=0 и, значит, его область сходимости есть непустое множество.
Теорема
Абеля: Если
степенной ряд (1.2) сходится при некотором ![]() ,
где
,
где![]() -число,
не равное нулю, то он сходится абсолютно
при всех значениях x таких,
что
-число,
не равное нулю, то он сходится абсолютно
при всех значениях x таких,
что ![]() Наоборот,
если ряд (12) расходится при
,
то он расходится при всех значениях x таких,
что
Наоборот,
если ряд (12) расходится при
,
то он расходится при всех значениях x таких,
что ![]()
Свойства степенных рядов:
Пусть (-R, R) – интервал сходимости степенного ряда (1.2), тогда:
1. Степенной ряд сходится равномерно на любом отрезке, содержащемся в (-R, R).
2. Сумма S(x) степенного ряда является непрерывной функцией в интервале (-R, R).
3. Степенной ряд внутри интервала сходимости можно почеленно дифференцировать.
4. Можно почеленно интегрировать на любом отрезке рассположенном в (-R, R).
5. Степенные ряды можно почленно складывать, вычитать, умножать, где у них общая область сходимости.
30. Аналитические функции. Ряд Тейлора.
Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.
Пусть
функция ![]() бесконечно
дифференцируема в некоторой окрестности точки
бесконечно
дифференцируема в некоторой окрестности точки ![]() .
Формальный ряд
.
Формальный ряд

называется рядом
Тейлора функции ![]() в
точке
.
в
точке
.
В случае, если
 ,
этот ряд также называется рядом Макло́рена.
,
этот ряд также называется рядом Макло́рена.Если есть аналитическая функция в любой точке a, то её ряд Тейлора в любой точке области определения сходится к в некоторой окрестности .
Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности . Например, Коши предложил такой пример:
![]()
У этой функции все производные в нуле равны нулю, поэтому коэффициенты ряда Тейлора в точке равны нулю.
Аналити́ческая функция (действительного переменного) — функция, которая совпадает со своим рядом Тейлора в окрестности любой точки области определения.
Аналитическая
функция (комплексного переменного) —
функция комплексного переменного ![]() (где
(где ![]() и
и ![]()
Для вещественной и мнимой части этой функции в каждой точке
 выполняются условия
Коши — Римана (аналитичность
в смысле Коши — Римана);
выполняются условия
Коши — Римана (аналитичность
в смысле Коши — Римана);Ряд Тейлора функции в каждой точке
 сходится
и его сумма равна
сходится
и его сумма равна  (аналитичность
в смысле Вейерштрасса);
(аналитичность
в смысле Вейерштрасса);Интеграл
 для
любой замкнутой кривой
для
любой замкнутой кривой 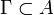 (аналитичность
в смысле Коши)
(аналитичность
в смысле Коши)
Свойства
Арифметические свойства
Если
и ![]() аналитичны
в области
аналитичны
в области ![]()
Функции
 ,
,  и
и  аналитичны
в
аналитичны
в  .
.Если в области не обращается в ноль, то
 будет
аналитична в
будет
аналитична в
Если
 в
области
не
обращается в ноль, то
в
области
не
обращается в ноль, то 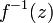 будет
аналитична в
.
будет
аналитична в
.
Аналитическая функция бесконечно дифференцируема в своей области аналитичности. Обратное в общем случае неверно.
Если множество нулей аналитической в односвязной области функции имеет в этой области предельную точку, то функция тождественно равна нулю.
