2.2. Определение основных кинематических параметров кривошипных машин

П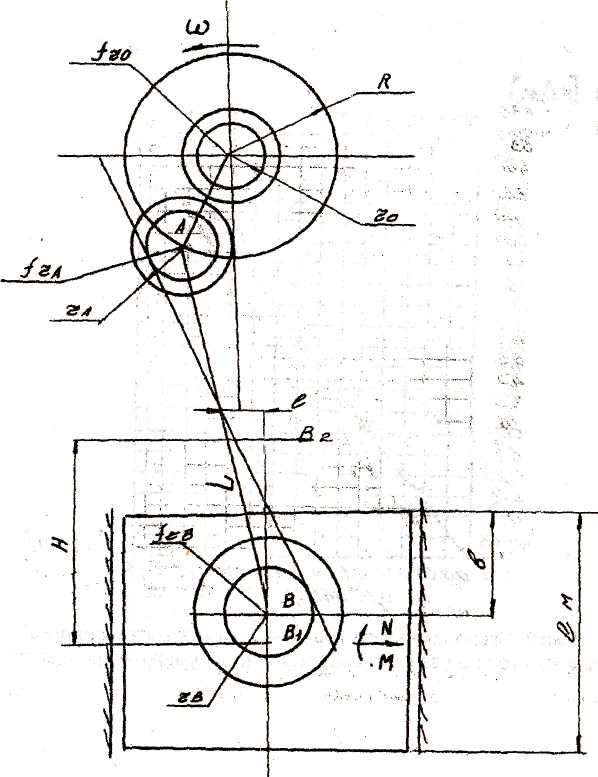 ри проектировании кривошипных машин необходимо устано­вить их кинематические параметры, т.е. определить законы изме­нения перемещений, скоростей и ускорений исполнительного звена - ползуна, найти максимальные значения этих параметров, а также их значения в период рабочего хода (рисунок 2.1.).

Рисунок 2.1. Кинематическая схема кривошипно-ползунного механизма

Путь ползуна определяется следующей зависимостью:

S_α = R[(1-cosα)+(λ/4)(1-cos2α)], (9)

S_α =70[(1-cos5)+(0,1/4)(1- cos2×5)]=0,24 см.

d₀=0,14√Р×10^-3=0,14√0,4=0,09 м,

R=0,08×d₀=0,08×0,09=0,007 м

и рассматривается через 5-10° угла α.

Скорость ползуна пресса определяется по формуле:

V = πRn_o/30(sinα +(λ/2)sin2α), (10)

V =3,14×0,7×15/30(sin5+(0,1/2) sin2×5) = 0,1 м/с

и рассчитывается через 5-10°α,

где n₀ - число оборотов кривошипа.

Ускорение ползуна определяется формулой:

j = (πRn₀/30)²R(cosα+λ cos2α),

j = (3,14×0,7×15/30)²×0,7(cos5+0,1 cos2×5) = 0,93 м/с² .

2.3. Определение крутящего момента

Крутящий момент на коленчатом валу реального механизма (с учетом сил трения):

M_k = Pm_k = P(m_k^u + m_k^f), (12)

где m_k^u = R(sinα +(λ/2)sin2α); (13)

m_k^u =0,7(sin5+(0,1/2) sin2×5=0,06 м.

С незначительной погрешностью m_k^f можно принять незави­сящим от α:

m_k^f = f[(1+λ)r₀+λ r_a+ r₀(1+(l₀/l_k)+ r₀(l₀/l_k)], (14)

m_k^f =0,03[(1+0,1)0,045+0,1×0,4+0,045(1+(0,18/0,26)+0,045(0,18/0,26)]=0,026 м.

М_k = 400(0,06+0,03) = 36 кНм.

2.4. Расчёт коленчатого вала

В зависимости от типа пресса выбирают конструкцию привода главного вала, который может быть одноколенчатым, двухколенча­тым, эксцентриковым, кривошипным. По номинальному усилию пресса на основании имеющихся эмпирических соотношений (рисунок 2.2.) определяют размеры вала. Полученные размеры округляют и выбирают материал вала (табл.9) [2].

Р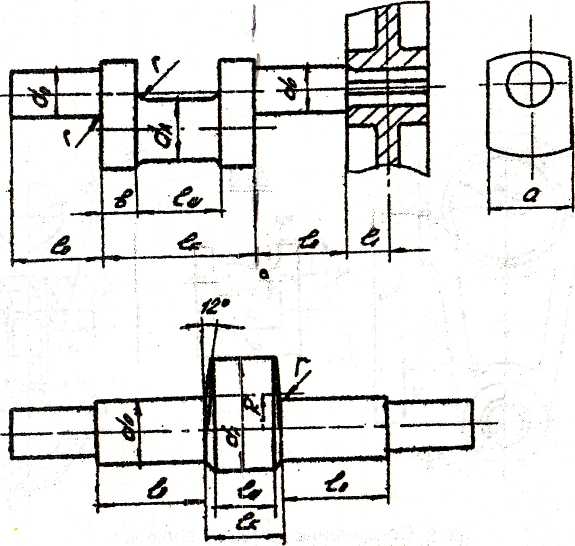 исунок 2.2. Размеры коленчатых валов:

а - одноколенчатых;

б - эксцентриковых;

Расчетным является сечение В-В

Усилие, допускаемое прочностью коленчатого вала, в сече­нии В-В

P_a= (15) P_a ³×275/1,3×0,8√0,004×0,18²×1,65+2,5(0,5×0,026+0,085×0,09²) =155кНм

Коэффициенты n и К_э принимаются по табл.8[2]; Ф_σ^в и Ф_τ^в опре­деляются по графикам, m_k - по формулам (13),(14) значения угла α_н принимаются по табл.14[2].

Максимальное нормальное напряжение:

σ_max= , (16)

где M_из= (l₀+l_k/2)×P_a=(0,18+0,26/2)× 155 = 49,5 кНм,

σ_max= = 650 МНм.

Максимальное касательное напряжение:

τ_max=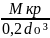 , (17)

τ_max= = 133,7 МНм.

Коэффициент запаса прочности на изгиб:

n_σ = , (18)

n_σ = = 0,37,

где σ_a - амплитуда цикла

σ_a = σ_max/2 = 650/2= 325,04 МНм, (19)

σ_m – среднее напряжение цикла

σ_m= 0. (20)

Коэффициент запаса прочности по касательным напряжениям:

n_τ =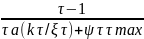 , (21)

n_τ = = 1,1.

τ_a=τ_max/2 , (22)

τ_a= 133,7/2 = 66,8 МНм.

τ_m = τ_max/2. (23)

Общий коэффициент запаса прочности:

N= , (24)

n= ,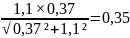

где Ψτ, Ψ_σ - коэффициенты, учитывающие влияние постоянной составляющей цикла на усталостную прочность (см. табл.9) [2];

ξ_σ , ξ_τ - масштабный фактор (табл.10) [2];

k_σ, k_τ - коэффициенты эффективной концентрации напряжений (табл.11) [2].