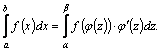- •19Достаточное услоие. Первый признак.
- •21.Точка перегиба. Достаточное и необходимое условия
- •Достаточное условие точки перегиба
- •26.2. Формула Тейлора для произвольной функции
- •23.Первообразная и неопределенный интеграл, их свойства
- •25Дробно-рациональная функция типы простейших алгебраических дробей и их интегрирование
- •26 27.Определенный интеграл римана, интегральная сумма, геом интерпритация, свойства
26 27.Определенный интеграл римана, интегральная сумма, геом интерпритация, свойства
Пусть
действительная функция f(x)
одного переменного x
определена на отрезке [a,
b].
Если существует предел I
интегральных
сумм Римана
![]() где
где ![]()
![]()
![]() k=1,…,n,
при
max∆a→0
(т.е. для любого ε
> 0 существует такое δ
> 0, что при max∆a<δ
верно
неравенство | S
–I
|
<
ε),
то I
называют
определённым интегралом Римана от
функции f
по отрезку [a,
b]
и обозначают
k=1,…,n,
при
max∆a→0
(т.е. для любого ε
> 0 существует такое δ
> 0, что при max∆a<δ
верно
неравенство | S
–I
|
<
ε),
то I
называют
определённым интегралом Римана от
функции f
по отрезку [a,
b]
и обозначают

Необходимым и достаточным условием интегрируемости f(x) на [a, b] в смысле Римана является ограниченность f(x) на [a, b] и равенство нулю меры Лебега множества всех точек разрыва f(x) на [a, b].
По
определению полагают, что ![]() а при a>b
а при a>b
![]()
Свойства интеграла Римана.
1)
Линейность: из интегрируемости на
[a,
b]
каждой из функций f(x)
и g(x)
следует, что для любых чисел α
и
β
функция
(α
f(x)
+ βg(x))
интегрируема на [a,
b]
и выполняется равенство
![]()
2) Из интегрируемости на [a, b] каждой из функций f(x) и g(x) следует интегрируемость на [a, b] их произведения f(x)g(x).
3)
Из интегрируемости на отрезке [a,
b]
функции f(x)
следует её интегрируемость на любом
подотрезке
![]()
4)
Аддитивность: из интегрируемости функции
f(x)
на каждом из отрезков [a,
b]
и [b,
c]
следует её интегрируемость на
[a,
c]
и равенство ![]()
5) Если функция f(x) интегрируема на [a, b] и все её значения принадлежат отрезку [A, B], а функция φ(x) непрерывна на [A, B], то сложная функция φ(f(x)) интегрируема на [a, b].
6) Если функции f(x) и g(x) интегрируемы на [a, b] и f(x) ≥ g(x) всюду на [a, b], то
7)
Из интегрируемости функции f(x)
на [a,
b]
следует интегрируемость на [a,
b]
функции |f(x)|
и оценка ![]()
Рассмотрим
функцию y
= f(x),
которая определена на отрезке [a;
b].
Разобьем отрезок [a;
b]
на n
частей
![]() точками
точками
![]() .
Обозначим
.
Обозначим
![]() ,
а точки
,
а точки
![]() будем
выбирать так, чтобы
будем
выбирать так, чтобы
![]() при
при
![]() .
Внутри каждого отрезка
выберем
точку
.
Внутри каждого отрезка
выберем
точку
![]() .
При
озвученных условиях существует множество
способов выбора точек
и
.
При
озвученных условиях существует множество
способов выбора точек
и
![]() .
Интегральной
суммой
функции y
= f(x)
для данного разбиения отрезка [a;
b]
и данного выбора точек
называют
выражение
.
Интегральной
суммой
функции y
= f(x)
для данного разбиения отрезка [a;
b]
и данного выбора точек
называют
выражение


Для конкретного разбиения отрезка [a; b] и выбора точек мы получим свою интегральную сумму. То есть, мы имеем множество интегральных сумм для различных вариантов выбора и .
Число
![]() называется
пределом
интегральных сумм
называется
пределом
интегральных сумм
![]() при
,
если для любого сколь угодно малого
положительного ипсилон
при
,
если для любого сколь угодно малого
положительного ипсилон
![]() существует
такое сколь угодно малое положительное,
зависящее от ипсилон, дельта
существует
такое сколь угодно малое положительное,
зависящее от ипсилон, дельта
![]() ,
что как только
,
что как только
![]() ,
то при любом выборе точек
справедливо
неравенство
,
то при любом выборе точек
справедливо
неравенство
![]() .
.
Функция
y
= f(x)
называется интегрируемой
на отрезке
[a;
b],
если существует конечный предел ее
интегральных сумм при
,
это значение предела называют определенным
интегралом Римана
и обозначают
 .
Числа
a
и b
называются нижним
и верхним пределом интегрирования
соответственно, f(x)
называется подынтегральной
функцией,
x
– переменной
интегрирования.
Значение
определенного интеграла не зависит от
переменной интегрирования, то есть,
.
Числа
a
и b
называются нижним
и верхним пределом интегрирования
соответственно, f(x)
называется подынтегральной
функцией,
x
– переменной
интегрирования.
Значение
определенного интеграла не зависит от
переменной интегрирования, то есть,

Теорема о среднем
Пусть
функция
непрерывна
на отрезке
![]() .
Тогда существует такая точка
.
Тогда существует такая точка
![]() ,
что
,
что

Доказательство.
Заметим для начала, что функция
интегрируема
на
,
так что интеграл в левой части доказываемого
равенства существует. Поскольку функция,
непрерывная на отрезке, принимает на
нём в некоторых точках
![]() и
и
![]() своё
наименьшее и наибольшее значения
своё
наименьшее и наибольшее значения
![]() и
и
![]() ,
то
,
то
![]() при
всех
при
всех
![]() .
Согласно неравенству (3.4),
величина
.
Согласно неравенству (3.4),
величина
![]() удовлетворяет
неравенству
удовлетворяет
неравенству

и,
следовательно, является промежуточным
значением между
![]() и
и
![]() .
Но непрерывная функция принимает любое
своё промежуточное значение в некоторой
точке отрезка, значит, существует такая
точка
,
что
.
Но непрерывная функция принимает любое
своё промежуточное значение в некоторой
точке отрезка, значит, существует такая
точка
,
что

Умножая
последнее равенство на
![]() ,
получаем утверждение теоремы.
,
получаем утверждение теоремы.
28 Определённый интеграл с переменным верхним пределом
Пусть f(x) – непрерывная на отрезке [a, b] функция, а F(x) – её первообразная. Рассмотрим определённый интеграл
![]() (47)
(47)
где
![]() ,
,
а через t обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х, которую обозначим через Ф(х), т.е.
![]() (48)
(48)
Докажем, что функция Ф(х) является первообразной для f(x) = f(t). Действительно, дифференцируя Ф(х), получим
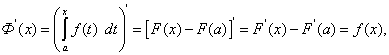
так как F(x) – первообразная для f(x), а F(a) – постояная величина.
Функция Ф(х) – одна из бесконечного множества первообразных для f(x), а именно та, которая при x = aобращается в нуль. Это утверждение получается, если в равенстве (48) положить x = aи воспользоваться теоремой 1 предыдущего параграфа.
теорема:
производная
интеграла с переменным верхним пределом
от непрерывной функции равна подынтегральной
функции, в которой переменная интегрирования
заменена верхним пределом:

Доказательство. По определению производной
 где
где
![]()
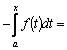 [первый
интеграл представим в виде суммы двух
интегралов, пользуясь свойством
аддитивности]=
[первый
интеграл представим в виде суммы двух
интегралов, пользуясь свойством
аддитивности]=![]()
![]() [по
теореме о среднем]=
[по
теореме о среднем]=![]() где
где
![]()
Тогда![]() следует
из определения непрерывной функции,
т.к. при
следует
из определения непрерывной функции,
т.к. при
![]()
![]() .
Таким образом,
.
Таким образом,

Это
значит, что интеграл с переменным верхним
пределом
![]() является
первообразной для функции
является
первообразной для функции
![]() .
.
29 Формула Ньютона–Лейбница
Теорема.
Если
![]() – какая–либо первообразная для
непрерывной функции
,
то
– какая–либо первообразная для
непрерывной функции
,
то
Доказательство.
Пусть
–некоторая
первообразная функции
.
Но
![]() – также первообразная для
,
а любые две первообразные данной функции
отличаются на постоянную, то есть можно
записать:
– также первообразная для
,
а любые две первообразные данной функции
отличаются на постоянную, то есть можно
записать:
|
(4) |
Это
равенство справедливо для любых
![]() .
Положим
.
Положим
![]() :
:
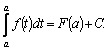 Но
Но
 ,
поэтому
,
поэтому
![]() ,
,![]() .
Полагая в (4) x=b
и подставляя значение C,
получим
.
Полагая в (4) x=b
и подставляя значение C,
получим
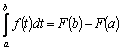 Переобозначив переменную интегрирования
,
получим формулу
Ньютона – Лейбница:
Переобозначив переменную интегрирования
,
получим формулу
Ньютона – Лейбница:
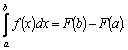
При вычислении определенных интегралов будем записывать:
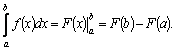
30.определенный интеграл римана, методы вычисления: интегрирование по частям, замена переменных
Замена переменной в определенном интеграле
Теорема.
Пусть
дан интеграл
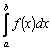 ,
где
непрерывна на
,
где
непрерывна на
![]() .
Введем новую переменную
.
Введем новую переменную
![]() ,
связанную с
равенством
,
связанную с
равенством
![]() .
Если
.
Если
1)
![]()
2)
![]() и
и
![]() непрерывны на
непрерывны на
![]() ,
,
3)
при изменении z от α до β значения
не выходят за пределы отрезка
![]() то
то
|
(5) |
Доказательство.
Пусть
–первообразная
для функции
,
то есть
![]() .
Тогда по формуле Ньютона–Лейбница
.
Тогда по формуле Ньютона–Лейбница
|
(I) |
покажем,
что функция
![]() является первообразной для функции
является первообразной для функции
![]() :
:
![]() =[по
правилу дифференцирования сложной
функции] =
=[по
правилу дифференцирования сложной
функции] =![]() Тогда по формуле Ньютона–Лейбница
Тогда по формуле Ньютона–Лейбница
|
(II) |
Интегрирование по частям в определенном интеграле
Формула
интегрирования по частям в определенном
интеграле выводится так же, как и для
неопределенного интеграла, и имеет вид
![]()