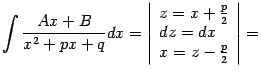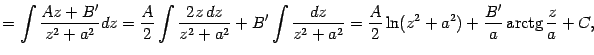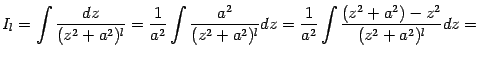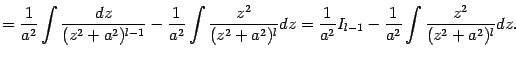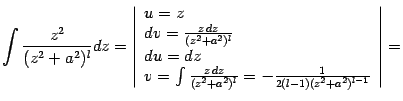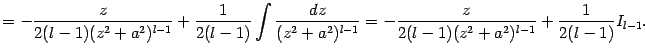25Дробно-рациональная функция типы простейших алгебраических дробей и их интегрирование

Функция называется рациональной функцией, или рациональной дробью, если она представляет собой отношение двух многочленов и :

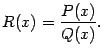
Пусть степень многочлена равна , а степень равна , то есть

где и . Разделив числитель и знаменатель на число , мы получим, что коэффициент при старшей степени в знаменателе равен 1. Для дальнейшего нам будет удобно предполагать, что эта операция уже произведена, то есть что . Далее мы будем предполагать, что все коэффициенты и  -- вещественные числа.

Если , то дробь называется правильной, а если , то неправильной. Если дробь неправильная, то её числитель можно поделить на знаменатель , получив при этом частное и остаток , степень которого меньше . Это означает, что

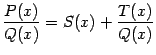
или что

где  -- некоторый многочлен, называемый целой частью рациональной дроби . Если остаток тождественно равен 0, то многочлен делится на без остатка, и функция является многочленом, то есть совпадает со своей целой частью .

С интегрированием целой части дроби , то есть многочлена , не возникает никаких проблем, так что в дальнейшем мы можем заняться выяснением способов интегрирования лишь правильных рациональных дробей.

Для нахождения частного и остатка можно применять алгоритм деления многочленов "столбиком". Приведём пример.

        Пример 2.9   Разделим с остатком  -- многочлен третьей степени -- на бином  -- многочлен первой степени:

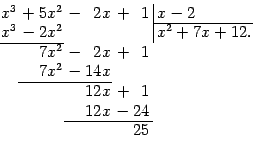
Таким образом, мы представили неправильную рациональную дробь в виде

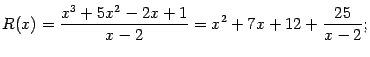
здесь мы получили частное и остаток  -- многочлен нулевой степени, то есть постоянную.     

интегрирование простейшей дроби первого типа сводится к применению табличной формулы:

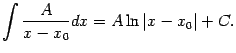
Интегрирование простейшей дроби второго типа сводится к табличной формуле после замены вида :

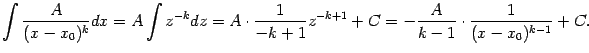
Интегрирование простейшей дроби третьего типа выполняется с помощью выделения в знаменателе полного квадрата и разбиения интеграла на два слагаемых, которые вычисляются как было показано выше в примере:

где 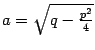и . Осталось подставить :

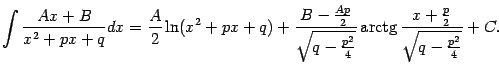
Разумеется, заучивать полученную формулу не нужно, а нужно научиться выполнять для конкретных примеров все указанные преобразования.

Интегрирование простейшей дроби четвёртого типа также начинается с выделения в знаменателе полного квадрата и замены , после чего интеграл приводится к виду , где . Разбиваем этот интеграл на два слагаемых:

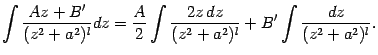
Первый из интегралов легко вычисляется заменой :

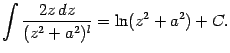
Для второго интеграла,

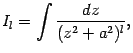
мы можем получить формулу понижения степени, если преобразуем его следующим образом:

	(2.4*)
	(2.5)

Последний интеграл преобразуем, применив формулу интегрирования по частям:

Подставив это выражение в (2.4*), получаем:

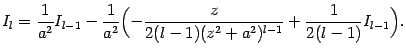
Это и есть формула понижения степени, сводящая вычисление интеграла к вычислению интеграла . Если , то интеграл  -- табличный; если же , то для вычисления нужно снова применить формулу понижения степени, и так до тех пор, пока не получится тот же табличный интеграл .