1. Подготовка данных обмера магнитопровода

Подготовка данных обмера магнитопровола включает в себя определение следующих показателей:

1. площади полюса в воздушном зазоре ( Qδ), ;

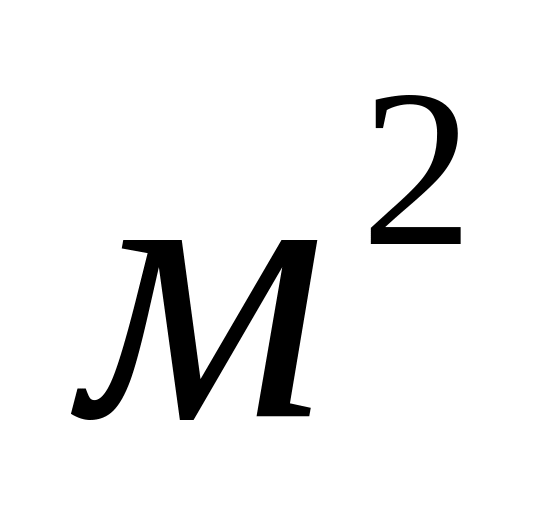2. площади полюса в зубцовой зоне статора(Qz), ;

3. площади поперечного сечения спинки статора(Qc), ;

4. площади паза в свету(Qп), ;

Первый три площади необходимы для расчета магнитных нагрузок в магнитной цепи асинхронного двигателя, последняя - для расчета сечения обмоточного провода.

В воздушном зазоре сопротивление магнитному потоку Ф по все площади полюса Q равномерное, , поэтому:

, (1)

где - полюсное деление (ширина полюса в воздушном зазоре), м;

- расчетная длина статора, без учета каналов охлаждения, м.

Если каналов нет то =l, где l- полная длинна сердечника статора, мм.

, (2)

где Р – количество пар полюсов, шт.; D- внутренний диаметр сердечника статора, мм.

, (3)

где f- частота питающей сети, Гц; n- частота вращения магнитного поля статора, .

Рассчитаем количество пар полюсов:

Зная количество пар полюсов рассчитаем ширину полюсного деления в воздушном зазоре:

.

Определяем площадь полюса в воздушном зазоре:

.

В зубцовой зоне статора магнитный поток протекает только по листам электротехнической стали, так как ее магнитная проницаемость много больше, чем изоляция листов. Следовательно длина магнитопровода l, а значит и площадь полюса сократятся на площадь занимаемую изоляцией.

Отсюда будет равна произведению активной площади зубца на их количество в полюсе,

, (4)

где - площадь одного зубца, ;

- количество зубцов под полюсом, шт.

, (5)

где - активная длина магнитопровода (без изоляции листов), м.

- расчетная средняя ширина зубца, м.

, (6)

где - коэффициент, учитывающий заполнения пакета магнитопровода сталью, зависящий от рода изоляции и толщины листов стали. Из таблицы 2 [1] выбираем =0,95. Тогда активная длина магнитопровода будет равна:

Средняя ширина зуба определяется из выражения, м

, (7)

где и - ширина зуба, соответственно, в узком и широком местах, м.

Где находится узкое и широкое место у зуба зависит от размеров магнитопровода и формы паза, поэтому вначале находятся размеры зуба у расточки статора , а затем у его основания .

Ширина зуба у расточки, м

, (8)

где е- высота усика паза, мм;

- меньший размер ширины паза, мм;

26. число пазов, шт.

Рассчитаем ширину зуба у расточки:

Ширина зуба у основания, м

(9)

где h- полная высота паза, мм;

b- больший размер ширины паза, мм.

Рассчитаем ширину зуба у основания:

Из выполненных расчетов следует, что узкое место зуба будет у его основания, а широкое у магнитопровода асинхронного двигателя (АД).Тогда:

Количество зубцов под полюсом определяется из выражения, шт:

, (10)

Определяем площадь одного зуба:

.

Зная площадь одного зуба и количество зубцов под полюсом определим площадь полюса в зубцовой зоне статора:

.

Площадь магнитопровода в спинке статора, перпендикулярная магнитному потоку Ф, равна произведению ее высоты на активную длину магнитопровода ,

, (11)

, (12)

Площадь паза в свету требуется при расчете сечения обмоточного провода. Для ее определения площадь заданной формы паза разбивается осевыми линиями на простые фигуры: полуокружность с диаметром b^’, трапецию и еще одну полуокружность с диаметром b.

Тогда, площадь паза Q_п равна, мм²:

, (13)

где Q_т - площадь трапеции с основаниями b^’ и b и высотой h_т, мм;

Q_b’,Q_b – площади полуокружностей с диаметрами, соответственно b’ и b, мм².

Высота трапеции определяется по формуле:

(14)

мм.

Тогда, , мм²

, (15)

мм² .

Найдем площади полуокружностей b’ и b соответственно, мм²

, (16)

мм² .

, (17)

мм² .

Зная площади трапеции и полуокружностей, определяем площадь паза в свету

мм² .