Ионизирующее излучение, его взаимодействие с веществом / ЧМТПИ_лек_1_030919pub
.pdf
материалы С15-103,-161,-162 2019 без права распространения
Численные методы теории переноса ионизирующих излучений
Панин Михаил Петрович mppanin@mephi.ru 917-502-9888
Учебные
Осенний семестр 2019
Учебные материалы С15-103,-161,-162 2019 без права распространения
Цели
Знать:
Каким образом можно рассчитать количественные характеристики поля излучения для решения практических задач
Как выбрать наиболее эффективный метод расчета в зависимости от конкретной задачи
Технологию математического моделирования переноса излучения
Уметь:
Рассчитывать характеристики полей излучения с помощью метода математического моделирования
2
Структура курса
|
Метод Монте-Карло |
КР |
||
|
|
Введение в ММК |
||
|
|
|
||
|
|
Технология применения ММК для переноса |
|
|
|
|
|
нейтральных частиц |
БДЗ |
|
|
|
|
|
распространения |
|
ММК для переноса заряженных частиц |
|
|
|
Численные (детерминированные) методы |
|
||
права |
|
|
||
|
решения уравнения переноса |
|
||
2019 без |
|
|
||
|
|
Метод сферических гармоник |
|
|
161,-162 |
|
|
|
|
|
Метод моментов |
|
||
103,- |
|
|
Метод дискретных ординат |
|
15С |
|
|
||
- |
|
|
|
|
материалы |
|
Многогрупповое приближение |
Тест |
|
|
|
|||
|
|
|
||
Учебные |
Экзамен |
|
3
недели 10 – 1
недели 16 – 11
СК-8
Учебные материалы С15-103,-161,-162 2019 без права распространения
Методы решения задач радиационной физики
• |
Доза (человек, материал) |
|
Функционал поля излучения |
|
||
• Количество попаданий в детектор |
|
|
||||
|
|
|
|
|
||
• |
… |
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
, , Ω |
, , Ω |
Ω |
Больцмановский функционал |
|
|
|
|
|
|
|
∞ 0 4 |
|
|
|
||
Варианты:
1.Найти поле излучения , , Ω , а затем рассчитать интеграл
2.Сразу смоделировать искомый интеграл
1Детерминированные численные методы решения уравнения переноса
2Метод (Монте-Карло) статистического моделирования переноса излучения
4
Детерминированные/статистические методы
Детерминированные численные методы
Определение поля во всем фазовом пространстве
Высокая точность решения (5-6 значащих цифр)
Высокая скорость решения (для простых задач)
распространенияправабез |
Большие требования к памяти |
|
|
Приспособлены к малоразмерным задачам |
|
|
Приспособлены к простым граничным условиям |
|
2019 |
|
|
-162 |
Требуют упрощения зависимости от фазовых |
|
161, |
||
переменных |
||
103,- |
||
|
||
С15- |
|
|
материалыУчебные |
Трудности с нестационарными задачами |
|
|
Метод статистического моделирования
Любая геометрия и граничные условия Отсутствие упрощений физики взаимодействия
Решение нестационарных задач
Умеренные затраты памяти Хорошо приспособлен для параллельных вычисл.
Расчет небольцмановских функционалов
Расчет единственного функционала, а не поля
Стохастический характер результатов
Невысокая точность, медленная сходимость
5
Метод Монте-Карло
Учебные материалы С15-103,-161,-162 2019 без права распространения
6
1777 год
правараспространения |
|
|
|
|
= |
2 |
|
2019 без |
|
|
|
|
|
|
|
161,-162 |
|
|
|
103,- |
|
||
|
|
|
|
С15- |
Pierre-Simon |
|
|
материалыУчебные |
|
||
de Laplace |
|
||
|
|
||
|
1749 - 1827 |
|
|
История
Georges-Louis Leclerc, |
William Thomson, 1st |
|
Baron Kelvin |
||
Comte de Buffon |
||
1824-1907 |
||
1707-1788 |
||
|
||
|
1901 г.: моделирование |
|
|
||
|
параметров кинетической |
|
|
теории газов |
7
Учебные материалы С15-103,-161,-162 2019 без права распространения
Манхэттенский проект
Лос-Аламос, США, 1940-е
Enrico Fermi |
Nicholas |
Stanisław Marcin Ulam |
Johann von Neumann |
|
Constantine |
||||
1901-1954 |
1909-1984 |
1903-1957 |
||
Metropolis |
||||
|
|
|
||
|
1915-1999 |
|
|
«Метод Монте-Карло»
8
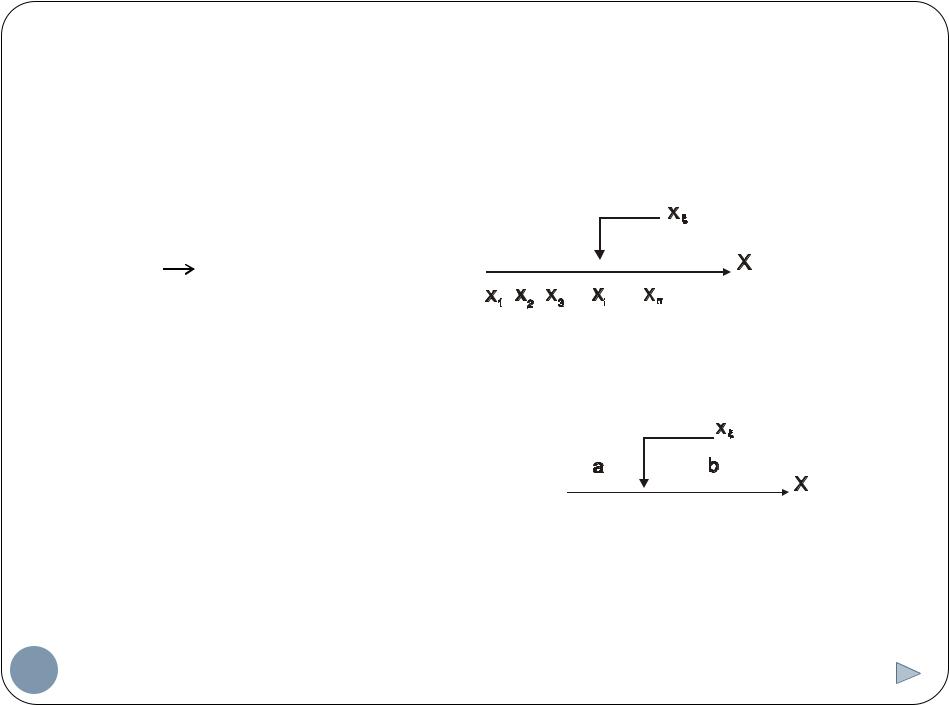
Случайные величины
Учебные материалы С15-103,-161,-162 2019 без права распространения
Дискретная случайная величина
|
|
|
x |
{xi}: x1, x2, …, xn |
= 1 |
|
||
|
|
<1 |
Непрерывная случайная величина на (a, b)
9
Учебные материалы С15-103,-161,-162 2019 без права распространения
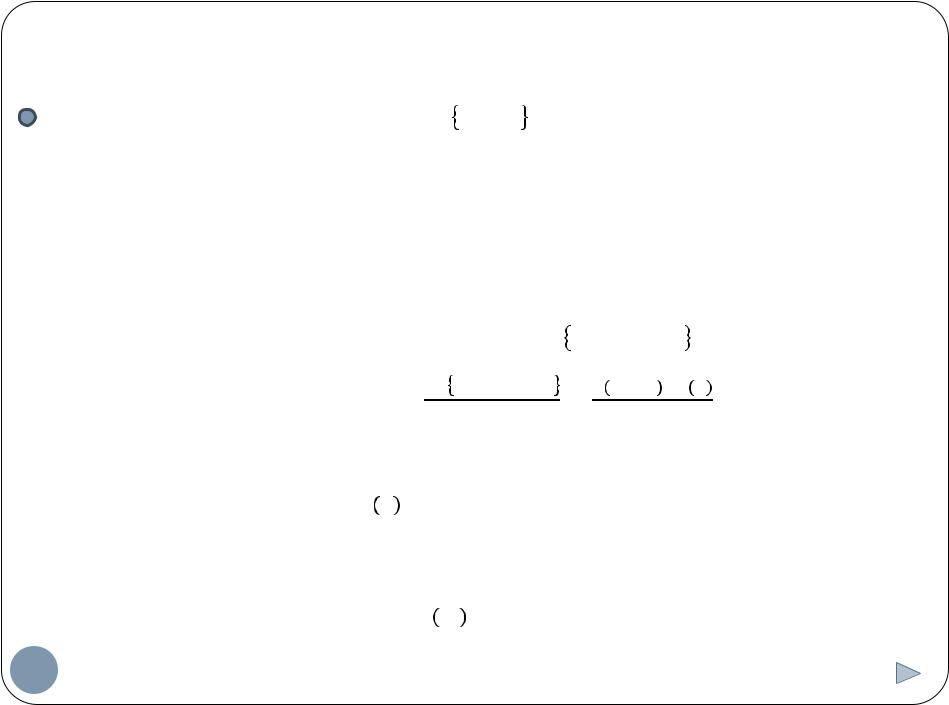
Функция распределения и плотность вероятности
Функция распределения: |
()=P |
|
|
≤ |
|
|
|
||
• Неотрицательная: |
() ≥ 0 |
|
|
|
•Неубывающая: 2 > 1 (2) ≥ (1)
• Значения на ±∞: (−∞) = 0 |
(∞) = 1 |
•Разница значений: 2 > 1: (2) − (1)=P 1 < ≤ 2
Плотность вероятности: |
() = |
< ≤ : |
= : ; |
|
|||
|
|
|
|
•Неотрицательная: () ≥ 0
:∞
• Нормированная: |
= 1 |
;∞
Связь функции распределения и плотности вероятности:
|
dF |
|
|
|
|
|
p(x) |
; |
( ) = |
′ |
′ |
||
dx |
||||||
|
;∞ |
|
10