6. Части графа. Связность графов.

Граф G называется связным, если для любой пары различных вершин этого графа существует цепь, соединяющая эти вершины.

Если для графа G можно указать пару различных вершин, которые не соединяются цепью (простой цепью), то граф называется несвязным.

Простейший пример несвязного графа — граф, содержащий изолированную вершину, простейший пример связного графа — любой полный граф.

Части графа.

Пусть дан граф G=(V, Е). Граф G’=(V’, Е’) называется его подграфом, если он получен из исходного путем удалением части вершин вместе с инцидентными им ребрами.

Например, если из графа представленного на рис.6 удалить вершины 3 и 5, то получим граф

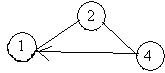
Всего из одного графа можно получить 2n подграфов.

Исходный граф по отношению к подграфу называется надграфом.

Маршрутом между вершинами v и w в графе G=(V, Е) называется последовательность ребер вида (v,x1), (x1,x2), (x2,x3),…, (xn-1,xn), (xn,w).

Например,

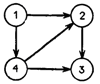
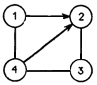
1,2), (2,3)-маршрут из первой вершины в третью.

Маршрут, у которого начальная вершина совпадает с конечной называется циклом. Например, на рис.8 (1,2), (2,3), (3,4), (4,1).

Вершина v называется достижимой из вершины w, если существует маршрут из w в v. Вершины v и w взаимнодостижимы если существует маршрут из v в w и маршрут из w в v. Для неориентированных графов достижимость вершин влечет взаимодостижимость.

Вершина графа для которой не существует достижимых вершин и которая не достижима из других вершин называется изолированной.

Очевидно, что вершина изолирована тогда и только тогда когда у нее нет инцедентных ребер.

Пример.

7. Операции над графами. Способы задания графов.

Способы задания графов и операции над графами

Граф G=(V,E) можно задать списком вершин и ребер. Можно задать и геометрически, нарисовав его на плоскости или любой другой поверхности и отождествив его вершины с точками на плоскости, а ребра с отрезками, соединяющими смежные (соседние) вершины.

Определение: Матрица смежности (соседства) вершин (p,q) – графа G=(V,E) с p вершинами есть квадратная симметричная матрица [p x p].

де aij:

- 1, если вершины Vi,Vj – соседние

- 0, в противном случае

Замечание: Всякому графу соответствует его бинарная симметричная матрица смежности. Всякая бинарная симметричная квадратная матрица с нулевой диагональю соответствует некоторому графу.

Определение: Матрица инциденций (соответствий) (p,q) – графа G=(V,E) с p вершинами и q ребрами есть [p x q] матрица

где Bij:

1, если вершина Vi? ребру ej

0, в противном случае

Замечание: для всякого графа можно построить соответствующую ему бинарную матрицу инциденций.

где Bij:

1, если вершина Vi? ребру ej

0, в противном случае

Замечание: для всякого графа можно построить соответствующую ему бинарную матрицу инциденций.

Операции над графами

1) удаление вершины v из графа G приводит к подграфу G-v графа G без вершины v и принадлежащих вершине v ребер.

2) Удаление ребра e из графа G=(V,E) при сохранении вершин приводит к подграфу G-e=(V,E – {e})

3) Добавление ребра e = (u,v) к графу G=(V,E), содержащему вершины u,v, приводит к графу G+e=(V,E?{e})