4. Степени и полустепени вершин. Теорема Эйлера о рукопожатии.

Теорема (Эйлер). Для того чтобы данный связный граф (не орграф, но, возможно, мультиграф без петель) был эйлеровым, необходимо и достаточно, чтобы степени всех вершин были четными.Данный связный граф будет полуэйлеровым тогда и только тогда, когда степени двух вершин будут нечетными, а степени остальных вершин – четными.

Доказательство этой теоремы начнем с так называемой леммы о рукопожатиях. Название этой леммы связано с тем, что эта лемма отвечает на следующий вопрос: У Вас собрались гости. Некоторые из них здороваются друг с другом посредством рукопожатий. Какими свойствами обладает число таких людей? Ответ дается следующей достаточно простой леммой.

Лемма о рукопожатиях. Число вершин в графе (или мультиграфе без петель), имеющих нечетную степень, четно.

Доказательство леммы. Заметим, что сумма степеней всех вершин в графе (или мультиграфе без петель) должна быть четной. Это следует из того, что если взять вершины, вообще не связанные друг с другом, то сумма степеней этих вершин равна нулю. Прибавляя любое ребро, которое связывает две вершины, увеличиваем сумму всех степеней на 2 единицы. Таким образом, сумма всех степеней вершин четна. Удаляя из этой суммы степени четных вершин, получим, что сумма степеней нечетных вершин, должна быть четной. Это значит, что само число таких вершин должно быть четным. Лемма доказана.

С точки зрения задачи о рукопожатиях это означает, что число гостей, которые поздоровались за руку нечетное число раз, должно быть четным.Перейдем к доказательству теоремы Эйлера.

5. Изоморфизм графов. Теорема Жордана.

В теории графов изоморфизмом графов и называется биекция между множествами вершин графов такая, что любые две вершины и графа смежны, если и только если вершины и смежны в графе . Здесь графы понимаются неориентированными и не имеющими весов вершин и ребер. В случае, если понятие изоморфизма применяется к ориентированным или взвешенным графам, накладываются дополнительные ограничения на сохранение ориентации дуг и значений весов. Если изоморфизм графов установлен, они называются изоморфными и обозначаются как .

Иногда биекция записывается в виде подстановки изоморфизма . Некоторые задачи обработки графов требуют не только проверки изоморфизма, но и выяснения его подстановки.

Отношение изоморфизма графов представляет собой отношение эквивалентности, определенное для графов, и позволяет произвести разбиение исходного класса всех графов на классы эквивалентности. Множество графов, изоморфных друг другу, называется классом изоморфизма графов (англ.), их число в зависимости от представляет собой последовательность A000088 в OEIS (1, 1, 2, 4, 11, 34, 156, 1044, 12346, ...).

В случае, если биекция отображает граф сам на себя (графы и совпадают), она называется автоморфизмом графа .

Граф Граф Изоморфизм между графами и Подстановка изоморфизма

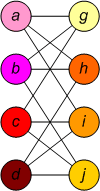
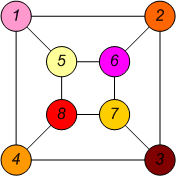
Изоморфизм графов общего вида

Графы и являются изоморфными, если путем перестановки строк и столбцов матрицы смежности графа удается получить матрицу смежности графа . Однако перебор всех возможных перестановок характеризуется вычислительной сложностью (при условии, что сравнение матриц смежности производится за время, не зависящее от , что обычно несправедливо и дополнительно увеличивает приведенную оценку), что существенно ограничивает применение подобного подхода на практике. Существуют методы ограниченного перебора возможных пар предположительно-изоморфных вершин (аналог метода ветвей и границ), однако они незначительно улучшают приведенную выше асимптотику