31. Постановка задачи динамического программирования

Пусть некоторая физическая управляемая система S находится в первоначальном состоянии s0 0. С течением времени ее состояние меняется и система приходит в конечное состояние sk k. С процессом изменения состояния системы связан некоторый численный критерий W. Необходимо так организовать процесс, чтобы критерий достиг оптимального значения.

Обозначим множество возможных управлений через U. Тогда задача состоит в том, чтобы из множества возможных управлений U найти такое управление U*, которое позволит перевести систему S из начального состояния s0 0 в конечное sk k так, что критерий W(U) принимает оптимальное значение W*.

32. Геометрическая интерпретация задачи динамического программирования

Геометрическая интерпретация задачи динамического программирования. Состояние экономической системы S можно описать числовыми параметрами, например расходом ресурсов, количеством вложенных средств и т.д. Назовем эти параметры координатами системы; тогда состояние системы можно изобразить точкой S, а переход из одного состояния S1 в другое S2 — траекторией точки S. Управление U означает выбор определенной траектории перемещения точки S из S1 в S2, т.е. установление определенного закона движения точки S.

Совокупность состояний, в которые может переходить система, называется областью возможных состояний. В зависимости от числа параметров, характеризующих состояние системы, область возможных состояний системы может быть различной. Пусть, например, состояние системы S характеризуется одним параметром, — координатой х. В этом случае изменение координаты, если на нее наложены некоторые ограничения, изобразится перемещением точки S по оси Ох или по ее участку. Следовательно, областью возможных состояний системы является совокупность значений х, а управлением — закон движения точки S из начального состояния s0 0 в конечное sk k по оси Ох или ее части (рис. 9.4.10).

Если состояние системы S характеризуется двумя параметрами (x1 и х2), то областью возможных состояний системы служит плоскость х1 0х2 или ее часть, а управление изобразится линией на плоскости, по которой точка S перемещается из s0 0 в sk k (рис. 9.4.11).

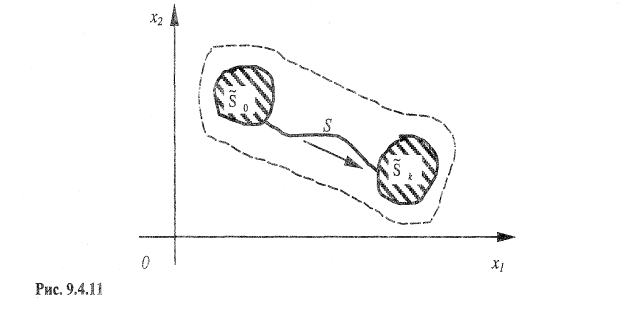
В общем случае, когда состояние системы описывается п параметрами хi (i =1,2,..., п), областью возможных состояний служит п -мерное пространство, а управление изображается перемещением точки S из какой-то начальной области s0 в конечную Sk по некоторой «траектории» этого пространства.

Таким образом, задаче динамического программирования можно дать следующую геометрическую интерпретацию. Из всех траекторий, принадлежащих области возможных состояний системы и соединяющих области s0 и Sk, необходимо выбрать такую, на которой критерий W принимает оптимальное значение.1

Объекты, с которыми имеет дело экономика, обычно снабжены своеобразными «рулями», с помощью которых осуществляется управление экономическими отношениями и процессами. Математически поведение такого объекта описывается уравнениями, куда входят и управляющие параметры, характеризуюгцие положение «рулей». При этом перед экономистом возникает задача отыскания наилучшего управления экономическими отношениями и процессами. Именно этой проблемой и занимается оптимальное. управление.