3.3. Интерпретация
Интерпретация Iисчисления предикатовKс областью интерпретациейM– это набор функций, который сопоставляет:
каждой предметной константе aэлементI(a)M;
каждому n-местному функторуfоперациюI(f):MnM.
каждому n-местному предикату Р отношениеI(P)Mn.
Для нас имеют смысл только интерпретированные предикаты, т. е. те, которым поставлены в соответствие некоторые отношения (для одноместных предикатов – свойства).
Пример.
Рассмотрим 3 формулы.
1. P(x,y)
2.
3.
В качестве области интерпретации возьмем
множество целых положительных чисел и
интерпретируем P(x,y)
как отношение
.
Тогда формула 1 – это предикат
.
Он принимает значение истинно при любыхa,bпринадлежащих
множеству целых положительных чисел,
если
.
Формула 2 – это предикат, который
принимает значение истинно при x=1,
т. е. он выражает свойство, что для каждого
положительного целого числаy
.
Формула 3 – это предикат, который всегда
будет истинен. Он выражает свойство:
существует положительное целое число
y, для которого
.
Формула называется истинной, если она выполняется на любом наборе элементов М.
Формула называется ложной, если она не выполняется на любом наборе элементов М.
Формула общезначима (тавтология), если она истинна в любой интерпретации.
Теорема:Любая выводимая в исчислении предикатов формула – общезначима.
3.4. Основные равносильности для предикатов
Пусть формулы А и В имеют одно и то же множество свободных переменных (в том числе и пустое).
Формулы А и В равносильны в данной интерпретации, если на любом наборе значений свободных переменных они принимают одинаковое значение (т. е. формулы выражают один и тот же предикат).
Формулы А и В равносильны на множестве М, если они равносильны во всех интерпретациях, заданных на множестве М.
Формулы А и В равносильны (
),если
они равносильны на всех множествах.
Для формул логики предикатов сохраняются все равносильности логики высказываний.
Перенос квантора через отрицание
В
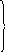ынос
квантора за скобки
|
|
Q– не зависит от х |
|
|
Q – зависит от х |
|
|
только в одну сторону! |
Пусть P(x) –xпошел в театр,Q(x) –xпошел в кино, тогда
.
Но
.
Аналогично, пусть P(x) –xделится на 2,Q(x) –xделится на 3, тогда
,
но
.
Перестановка одноименных кванторов
Перестановка разноименных кванторов
Переименование связанных переменных
х, у принадлежат одной предметной области
Отбрасывание квантора
Пример. Докажем общезначимость
формулы
.
Для этого надо показать, что формула
является теоремой исчисления предикатов.
Доказательство.
1.
- аксиома исчисления предикатов.
2.
- аксиома исчисления предикатов.
3. Для исчисления высказываний доказано
правило транзитивности:
4. Из 1 и 2 по правилу транзитивности получаем:
5. Введение квантора существования
(правило вывода исчисления предикатов
):
6. Введение квантора общности (правило вывода исчисления предикатов
):
7. Преобразуем связанную переменную {y/z}
8. Преобразуем связанную переменную {x/v}
Таким образом, теорема доказана.