6.3.2. Задания к главе 3
1. Изучить и выполнить все примеры главы 3.
2. Знать основные алгоритмы работы с массивами, уметь реализовать их на практике.
Создание и вывод элементов массива.
Суммирование элементов массива.
Поиск максимального и минимального элемента массива, вывод их значений, а также соответствующих индексов на экран.
Сортировка элементов массива.
Для двух заданных массивов построить третий, элементы которого:
есть и в первом, и во втором массиве одновременно;
есть в первом, но отсутствуют во втором;
есть во втором, но отсутствуют в первом;
есть или в первом, или во втором массиве.
3. Создать массив, элементы которого перечисляют животных зоопарка (всего 5-8 наименований) и распечатать их.
4. Проанализировать приведённый ниже скрипт: понять, что он описывает, как работает, что будет печатать на экране.
<?php
$photo=array("name"=>"dog.jpg", "size"=>"130k", "type"=>"image/jpeg", "description"=>"Фотография моей собаки");
while ($m=each($photo)) // Необходимо изучить работу функции each( )!
{
echo $m["key"];
echo " — ";
echo $m["value"];
echo "<br>";
}
?>
Выполнить скрипт и сравнить ваш прогноз с результатом его работы.
5. Создать скрипт, описывающий содержание цифрового семейного фотоальбома, в котором находятся несколько фотографий (например, 5) ваших родственников.
6. Проанализировать и выполнить приведённый ниже скрипт, предварительно предсказав результат его работы:
<?php
$flowers = array (
array('name'=>'magnolia', 'лепестки'=>'8', 'тычинки'=>'5',
'пестики'=>'2', 'цвет'=>'белый'),
array('name'=>'primula', 'лепестки'=>'10', 'тычинки'=>'5',
'пестики'=>'5', 'цвет'=>'алый'),
array('name'=>'campanula latifolia', 'лепестки'=>'10',
'тычинки'=>'5', 'пестики'=>'3', 'цвет'=>'фиолетовый')
);
for ($row=0; $row<3; $row++)
{
echo "|". $flowers[$row]["name"]. "|". $flowers[$row]["лепестки"]. "|".
$flowers[$row]["тычинки"]."| <br>";
}
?>
7. Изучить работу функции shuffle(). Написать скрипт, реализующей следующую задачу:
а. Турфирма имеет набор файлов (например, формата .jpg) с видами 10 российских городов;
б. При входе на сайт этой фирмы посетитель видит таблицу с видами трёх из этих городов, выбранных случайным образом.
Указание: таблицу отображать средствами HTML.
9. Создать двумерный массив, отображающий меню ресторана, где на первое – одно блюдо, на второе – одно блюдо, а на третье (десерт)– три возможных варианта блюд. Распечатать меню с помощью функции print_r().
Сделать то же самое для меню, где имеются по два варианта первых, вторых и третьих блюд.
10. Далее предлагаются задачи на обработку одномерных и двумерных численных массивов. При этом, значения исходных массивов необходимо задавать с помощью специальных функций – генераторов случайных чисел, сведения о которых необходимо самостоятельно получить из Интернета56.
Задачи на одномерные массивы:
Даны две точки
и
.
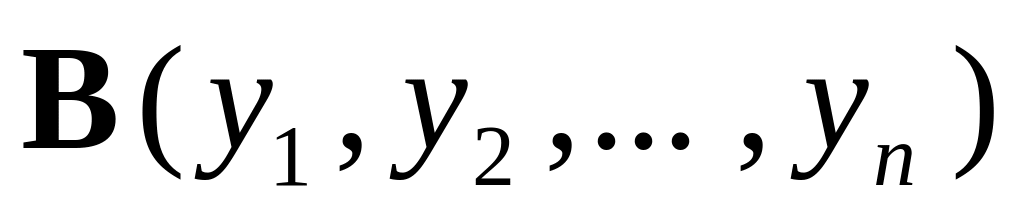Найти координаты и модуль вектора
.
Формула
и
.Определить координату точки А, являющейся началом вектора
,
если его конец совпадает с точкой
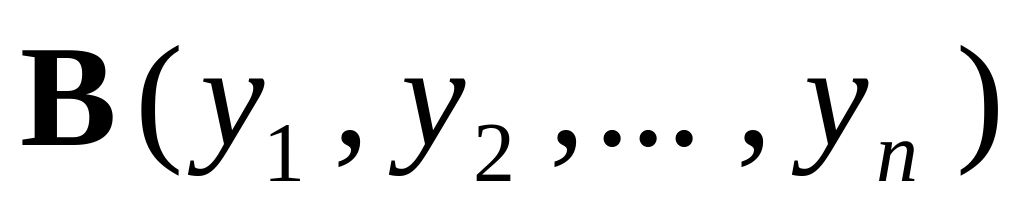.Даны две точки и . Найти координаты точки
делящей отрезок в данном отношении
.
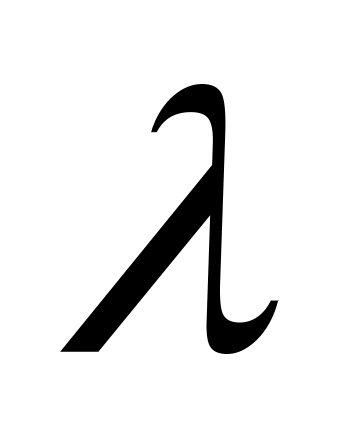Формула
.Даны вершины треугольника , и . Найти координаты точки
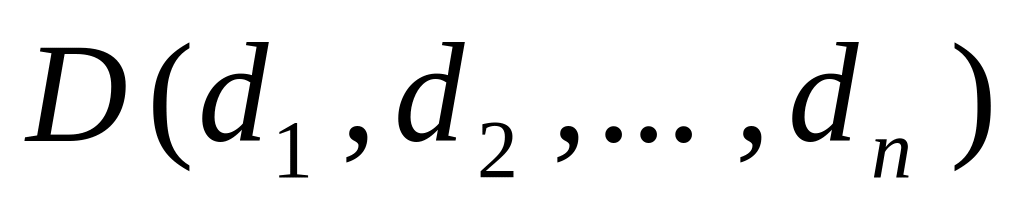пересечения биссектрисы угла А со
стороной ВС.
,
где
и длину биссектрисы АД.Нормировать вектор и найти его длину. Формула
.Найти скалярное произведение векторов
и
по формуле
.Найти угол между векторами и по формуле
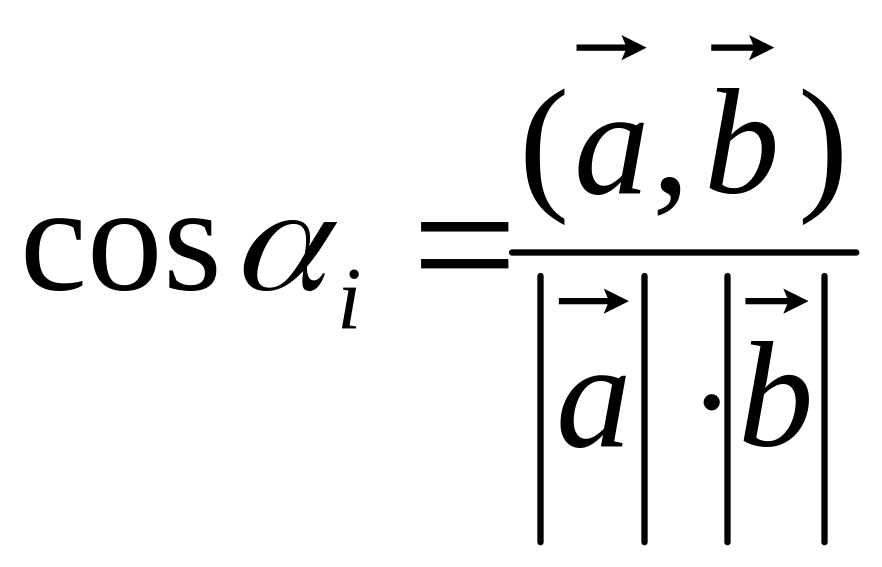
Проверить, что точки
,
,
и
являются вершинами параллелограмма,
трапеции или ромба.Даны векторы и . Найти вектор
Даны векторы и . Найти
и
.
Формула
и
Даны вершины треугольника , и . Определить является ли он остроугольным, прямоугольным, равнобедренным.
Найти длину медианы опущенной из вершины А на сторону ВС.
Даны три последовательные вершины параллелограмма , , . Найти его четвертую вершину и длины его диагоналей. Указание: Находите координаты точки пересечения диагоналей
,
где
Найти угол между диагоналями параллелограмма построенного на векторах и Указание: векторы диагоналей
и
.Проверить коллинеарность векторов и . Если они коллинеарны, то установить какой из них длиннее другого и во сколько раз. Как они направлены в одну сторону или в противоположные стороны? Указание:
Вычислить угол образованный медианами треугольника , и .
Имеется два отсортированных массива по неубыванию. Составить из них третий массив, объединив первые два, элементы которого расположить по неубыванию.
Дан вектор. Из него построить другой вектор, в котором нет нулевых элементов из первого.
Задачи на обработку многомерных массивов
Дано: матрица А размерности mxn и матрица В размерности mxn. Найти сумму матриц С=А+В.
Дано: матрица А размерности mxn. Найти транспонированную матрицу.
Дано: матрица А размерности mxn и матрица В размерности nхk. Найти произведение матриц С=А*В.
Просуммировать элементы строк матрицы размером mхn. Результат получить в одномерном массиве размером m.
Просуммировать элементы столбцов заданной матрицы размером mхn. Результат получить в одномерном массиве размером n.
Для заданной квадратной матрицы сформировать одномерный массив из ее диагональных элементов. Найти след матрицы, суммируя элементы одномерного массива.
Задана квадратная матрица. Переставить главную и побочную диагонали.
В матрице nxn найти количество отрицательных элементов побочной диагонали и произведение всех положительных элементов выше главной диагонали.
В матрице mхn найти минимальный элемент k-ого столбца и сумму положительных элементов ниже p-ой строки.
В матрице nxn найти произведение ненулевых элементов, расположенных ниже главной диагонали, и максимальный из элементов главной диагонали.
Найти максимальные элементы в каждом из столбцов матрицы А размером mхn и образовать из них новый одномерный массив С размерности n.
Найти произведение элементов матрицы mхn, удовлетворяющих условию А[i,j] <=2, и количество неотрицательных остальных элементов.
Найти минимальный среди положительных элементов матрицы mхn, лежащих слева от p-ого столбца, и произведение неотрицательных элементов в остальной части матрицы.
Найти минимальный элемент среди элементов p-oго столбца матрицы mхn и сумму элементов, лежащих ниже r-ой строки матрицы.
Найти количество неотрицательных элементов второго столбца матрицы nхn и минимальный элемент ниже побочной диагонали.
Преобразовать все элементы, расположенные в указанных строках матрицы nхn, по правилу: отрицательные элементы заменить на –1, положительные на +1, а нулевые оставить без изменения.
Найти минимальный среди положительных элементов матрицы nхn, расположенных выше главной диагонали и количество отрицательных элементов на главной диагонали.
Найти наибольший элемент главной диагонали матрицы nхn и его место в матрице, а также минимальный элемент побочной диагонали.
Найти сумму неотрицательных элементов, лежащих справа от р-oго столбца матрицы nхn и максимальный элемент на главной диагонали.
В каждой строке матрицы mхn выбирается элемент с наименьшим значением, затем среди этих чисел выбирается наибольшее. Указать элемент и его индексы.
Найти наименьшее из значений элементов столбца матрицы nхn, который обладает наибольшей суммой модулей элементов. Если таких столбцов несколько, то взять первый из них.
Дана квадратная матрица nxn. Получить квадратную матрицу того же порядка, в которой элемент равен 1, если соответствующий ему элемент исходной матрицы больше элемента, расположенного в его строке на главной диагонали, или, в противном случае, равен 0.
Среди элементов матрицы nxn найти максимальный - на главной диагонали и минимальный - на побочной диагонали. Определить их место в матрице.
В матрице nхn найти количество отрицательных элементов, расположенных на побочной диагонали и выше ее, а также максимальный элемент побочной диагонали.
В матрице nxn указать индексы всех элементов с наибольшим значением.
В матрице nxn все элементы с наименьшим значением заменить нулями.
В матрице nxn найти наибольший элемент, расположенный выше главной диагонали и наименьший ниже нее.
В матрице mхn поменять местами строку, содержащую элемент с наибольшим значением, со строкой, в которой расположен элемент с наименьшим значением. Если таких строк несколько, то поменять строки с наименьшими номерами.
Даны матрица nxn и число К (1<=K <=n). Столбец с максимальным по модулю элементом в К-той строке переставить с К-тым столбцом.
Найти наименьшее из значений элементов столбца, который обладает наибольшей суммой модулей элементов в матрице nхn.