
- •1.Предмет, цели и задачи эконометрики (э). Экон.Модель (эм), основные этапы построения экон.Модели.
- •2.Простая линейная регрессия. Классические предположения модели.
- •3.Стат.Оценивание парам плр по мнк. Св-ва оценок.
- •4.Проверка качества плр: значимость параметров, адекватность моделей. Прогнозирование.
- •5.Множественная линейная регрессия (млр). Классич. Предположения. Мнк-оценка параметров модели.
- •6.Свойства мнк-оценок млр. Теорема Гаусса-Маркова.
- •7. Проверка качества множественной линейной регрессии: значимость параметров, доверительные интервалы, адекватность модели. Прогнозирование.
- •8.Спецификация эконометрической модели: способы и диагностика отбора экзогенных переменных. Тесты Рамсея и Амемья.
- •9.Спецификация экономической модели: выбор формы зависимости нелинейной модели.
- •10. Проблема гетероскедастичности модели. Критерии её диагностики.
- •11.Взвешенный мнк в задаче оценивания параметров модели. Свойства оценок взвешенного мнк.
- •12.Проблема автокорреляции остатков модели. Последствия автокорреляции при использовании модели.
- •13. Критерий диагностики автокорреляции Дарбина-Уотсона.
- •14. Методы устранения автокорреляции
- •15. Проблема наличия мультиколлинеарности модели. Последствия наличия и диагностика мультиколлинеарности.
- •16. Методы устранения мультиколлинеарности.
- •17. Динамические модели с распределёнными лагами.
- •18. Структура лагов по Койку: Частные случаи (модель с неполной корректировкой и адаптивных ожиданий)
- •19. Понятие временного ряда(вр). Модель вр, основные задачи анализа вр. Методы сглаживания вр (скользящего среднего, экспоненциального сглаживания, последовательных разностей)
- •20. Стационарность вр. Характеристики корреляции уровней вр.
- •21. Стационарные модели временных рядов: авторегрессии, скользящего среднего арсс.
- •22. Системы одновременных эконометрических уравнений (соу). Структурная и приведенная форма соу (графическое и матричное представление)
- •23. Проблемы идентификации соу. Идентифицируемость уравнений соу.
- •24. Методы оценивания соу. Косвенный мнк. Двухшаговый мнк. Применимость и свойства оценок.
- •25. Современное состояние эконометрики. Примеры больших эконометрических моделей.
19. Понятие временного ряда(вр). Модель вр, основные задачи анализа вр. Методы сглаживания вр (скользящего среднего, экспоненциального сглаживания, последовательных разностей)
Временной
ряд – совокупность значений какого-либо
показателя за несколько последовательных
моментов или периодов времени, т.е.
t2-t1=
t3-t2=…=tn-tn-1=Δt.
Временнойрядобозначаетсяy(Δt),
y(2Δt),
…, y(nΔt)
y1,
y2,…,
yn(yT).
К этому классу относ модели: тренда
 ,
где T(t) – временной тренд параметрического
вида; сезонности
,
где T(t) – временной тренд параметрического
вида; сезонности
 ,
S(t)
– сезонная компонента,
- случайная компонента. Общее у временных
рядов то, что они объясняют поведение
временного ряда исходя изего пред знач.
,
S(t)
– сезонная компонента,
- случайная компонента. Общее у временных
рядов то, что они объясняют поведение
временного ряда исходя изего пред знач.
Задачи: 1) Сглаживание или выделение тренда по уровням временного ряда. 2) Прогнозирование.
Метод
скользящих средних. Он
основан на переходе от начальных значений
членов ряда к их средним значениям на
интервале времени, длина которого
определена заранее (m=2k+1). Если индивидуальный
разброс значений члена ВР ytоколо
своего среднего значения а
характеризуется
дисперсией σ2,
то разброс средней из tчленов
ВР (y1+y2+…+ym)/m
около того же значения а
будет
характеризоваться дисперсии σ2/t.
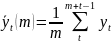
Метод экспоненциального сглаживания вычисляет взвешенную среднеарифметическую соседних уровней со стандартно заданным …
yt(λ)
=
 , |λ|<=1,
, |λ|<=1,
 т.е веса все время уменьшаются.
т.е веса все время уменьшаются.
Метод последовательных разностей.
Применяется если искомая ф-ия тренда имеет вид полинома:
Tt = c0+c1t+…+cmtm
Тогда вычисляют абсолютные цепные приросты уровней ряда и сравнивают их по величине.
 если
если ,
то вывод о линейности ф-и тренда. Если
они не равны, то продолжают вычислять
абсолютные приросты:
,
то вывод о линейности ф-и тренда. Если
они не равны, то продолжают вычислять
абсолютные приросты:
Если они ==, то => вывод о квадратической форме тренда. В противном случае продолжают вычислять конечные разности высших порядков и сравнивать их между собой.
20. Стационарность вр. Характеристики корреляции уровней вр.
Ряд
называют строго стационарным (в узком
смысле), если совместное
распределениеm наблюдений
 не зависит от сдвига по времени, т.е
совпадает с распределением
не зависит от сдвига по времени, т.е
совпадает с распределением
 .
Слабая стационарность (в широком смысле)
состоит в том, что дисперсия и ковариация
не зависит от момента времени:
.
Слабая стационарность (в широком смысле)
состоит в том, что дисперсия и ковариация
не зависит от момента времени:
 .
.
Значения
уровней временных рядов экономических
показателей могут содержать следующие
компоненты:- тренд
 (изменение,
определяющее общее направление развития,
основную тенденцию временного ряда);-
сезонную компоненту
(изменение,
определяющее общее направление развития,
основную тенденцию временного ряда);-
сезонную компоненту
 ;-
циклическую компоненту
;-
циклическую компоненту
 ;-
случайную составляющую
.
;-
случайную составляющую
.
Анализ временного ряда надо начинать с построения графика исследуемого показателя. По графику можно сделать предположение о наличии тренда и колебаний. Если амплитуда колебаний относительного среднего значения не меняется, то используют аддитивную модель; если же амплитуда возрастает (убывает), то используют мультипликативную модель.
Если присутствие тренда во временном ряду визуально прослеживается нечетко, то проводят статистическую проверку гипотезы о существовании тенденции, например, с помощью метода Фостера-Стюарта:
1)
Каждый уровень ряда
сравнивается со всеми предшествующими,
вычисляются вспомогательные характеристики
 и
и
 :
:

Т.е.
 ,
если
больше всех предшествующих уровней;
,
если
больше всех предшествующих уровней;
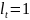 ,
если
меньше всех предшествующих уровней.
,
если
меньше всех предшествующих уровней.
2)
Вычисляется
 ,
,
 .
.
3)
Находится характеристика
 .
.
4)
С помощью критерия Стьюдента проверяется
гипотеза о том, что можно считать
случайной разность
 (т.е. ряд можно считать случайным, не
содержащим тренд). Для этого определяется
(т.е. ряд можно считать случайным, не
содержащим тренд). Для этого определяется
 ,
где
,
где
 – средняя квадратическая ошибка величины
D.
Расчетное значение критерия
– средняя квадратическая ошибка величины
D.
Расчетное значение критерия
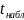 сравнивается с критическим значением
сравнивается с критическим значением
 для заданного уровня значимости
и числа степеней свободы
для заданного уровня значимости
и числа степеней свободы
 .
Если
.
Если
 ,
то гипотеза об отсутствии тренда
отвергается.
,
то гипотеза об отсутствии тренда
отвергается.
При
наличии у временного ряда тренда,
циклической и сезонной компонент
наблюдается корреляция между уровнями
временного ряда – автокорреляция.
Количественно автокорреляция
устанавливается с помощью линейного
коэффициента корреляции между уровнями
этого ряда и некоторым лагом
 .
Величина лага определяет порядок
коэффициента корреляции. Коэффициент
автокорреляции k-го
порядка вычисляется по формуле:
.
Величина лага определяет порядок
коэффициента корреляции. Коэффициент
автокорреляции k-го
порядка вычисляется по формуле:

где
 ,
,
 .
.
С
увеличением лага число пар уровней, по
которым рассчитывается коэффициент
автокорреляции, уменьшается. Считается
целесообразным использовать коэффициенты
автокорреляции с порядками:
 .
.
