
- •1. Матрицы и операции над ними
- •2. Определители 1,2 и 3 порядков
- •3.Миноры и алгебраические дополнения элементов.
- •4.Свойства определителей
- •5. Алгоритм Гаусса
- •6.Общие сведения о сист лин алг уравн
- •7. Элементарные преобразования систем. Теорема о равносильности систем при элементарных преобразованиях.
- •8.Исследование систем методом Гаусса.
- •9. Метод Крамера
- •10.Методы Гаусса и Жордана-Гаусса.
- •11. Обратная матрица и ее нахождение.
- •12.Матричный метод решения систем.
- •13.Ранг матрицы, теоремы о ранге.
- •14.Критерий совместности системы( теорема Кронекера-Капелли).
- •15.Критерий определенности системы линейных уравнений.
- •16.Системы с базисом. Приведение системы к системе с базисом методом Жордана-Гаусса.
- •17. Канонические системы. Преобразование однократного замещения.
- •18.Геометрические векторы и операции над ними.
- •19. Базисы и разложение векторов по базисам.
- •20.Скалярное произведение векторов и его свойства.
- •22. Прямая линия на плоскости.
- •23. Взаимное расположение прямых линий на плоскости
- •24.Окружность и эллипс(канонические уравнения).
- •25.Парабола(каноническое уравнение).
- •27.Исследование квадратичной функции.
- •28. Исследование дробно-линейной функции.
- •29. Примеры лз оптимизации.
- •30. Классификация задач лп
- •31. Графический метод решения задач лп:
- •32. Теоремы симплексного метода.
- •33. Алгоритм симплекс-метода:
10.Методы Гаусса и Жордана-Гаусса.
Если в процессе преобразования системы методом Гаусса появится хотя бы одно уравнение вида 0•х1 + … + 0•хn = b, с b ≠ 0, то система противоречива. Если встретится хотя бы одно уравнение с b = 0, то система имеет бесчисленное множество решений. Если уравнение вида 0•х1 + … + 0•хn = b, не будет вовсе, то система имеет единственное решение. Оно находится обратным ходом метода Гаусса. В последней ситуации определитель Δ(А) системы отличен от нуля.
Все сказанное относится и к методу полного исключения неизвестных – методу Жордана-Гаусса. (метод последовательного исключения неизвестных.)
Модификацией метода Гаусса является метод Жордана-Гаусса или метод полного исключения неизвестных. При этом методе каждое базисное неизвестное xi сохраня- ется только в одном каком-то уравнении с номером S (не обязательно, что S = i), а во всех остальных уравнениях оно исключается.
На практике при исследовании систем методом Гаусса или Жордана-Гаусса преобразованиям подвергают коэффициенты расширенной матрицы системы.
Для этого сначала заполняется исходная таблица. Далее выбирается разрешающий столбец. Это может быть любой столбец из коэффициентов при неизвестных. Пусть для определенности это будет столбец из коэффици- ентов при xk . Выберем в этом столбце разрешающий элемент, в качестве которого можно взять любой элемент столбца, отличный от нуля. Пусть это будет элемент ask. Тогда S-я строка объявляется разрешающей строкой.
После этого ведутся преобразования элементов исходной таблицы. На первом этапе элементы разрешающей строки остаются неизменными, а на месте всех коэффициентов разрешающего столбца, кроме коэффициента ask, записываются нули. Остальные элементы aij и bi преобразованной таблицы вычисляются по формулам:
аij(bi)=
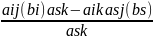
При этом исключилось неизвестное xk во всех уравнениях, кроме S – го.
На втором этапе в преобразованной таблице выбирается новый разрешающий элемент aqp' ≠ 0 в каком-то столбце р (будет исключаться неизвестное хр). При этом в случае метода Жордана-Гаусса неизвестное хр будет исключено во всех уравнениях, кроме q – го. В случае метода Гаусса хр будет исключено во всех уравнениях, кроме s – го и q – го. Элементы aij"и bi" строк новой таблицы, подлежащие преобразованиям, вычисляются по формулам, аналогичным последним 2м. В случае метода Гаусса преобразованиям подлежат все строки, кроме s – й и q – й; в случае метода Жордана-Гаусса – все строки, кроме q – й. Описанная процедура преобразования таблицы продолжается. Переход от одной таблице к другой называется итерацией (шагом, этапом).
Процесс метода Жордана-Гаусса продолжается, пока хотя бы в одной строке есть коэффициенты при неизвестных, отличные от нуля и не занимающие места разрешающих элементов предыдущих итераций.
11. Обратная матрица и ее нахождение.
Квадратная матрица А^-1 называется обратной к квадратной матрице А, если справедливы равенства
AX=XA=E
где Е – единичная матрица того же порядка, что и А.
У каждой матрицы А существует лишь одна обратная.
A*A^-1 = A^-1*A=E
Квадратная матрица А, определитель Δ(А) которой отличен от нуля, называется неособенной (невырожденной). В противном случае матрица называется особенной (вырожденной).
Теорема: каждая неособенная квадратная матрица имеет обратную, которая имеет вид:
A^-1= A^П
A^П
для особенной квадратной матрицы обратной не существует.
Если матрица системы n уравнений с n неизвестными неособенная, то система имеет единственное решение, которое представимо в матричном виде:
X= A^-1 *B
где Х – матрица-столбец из неизвестных, В- матрица-столбец из свободных членов системы, А-1 – обратная матрица к матрице системы.
