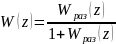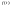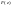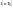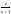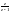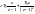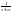II) Импульсные сау
Импульсный элемент – устройство для преобразования непрерывного сигнала в последовательность модулированных импульсов.
![]()
На выходе импульсного элемента:

где x[nT] - решетчатая функция
При x(t) = 1(t):
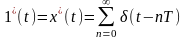
Импульсный элемент может быть представлен в виде двух частей:
-
простейший импульсный элемент
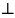 → решётчатая функция
→ решётчатая функция

-
формирователь импульса
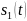 → определённая длительность каждого
импульса
→ определённая длительность каждого
импульса
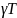
Импульсная САУ с АИМ (рис. 10.1, а):
Ошибка
рассогласования:

ИЭ – импульсный элемент
– приведённая непрерывная часть
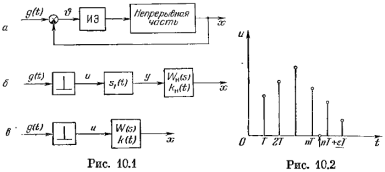
Частотные характеристики импульсных САУ
На
входе:
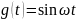
Преобразуется
в решётчатую функцию (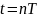 )
→
)
→
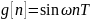
III) Математическое описание импульсного элемента
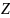 -преобразование
– преобразование является одним из
математических методов анализа и
проектирования дискретных систем.
Аппарат z-преобразования играет для
цифровых систем ту же роль, что и
преобразование Лапласа для непрерывных
систем.
-преобразование
– преобразование является одним из
математических методов анализа и
проектирования дискретных систем.
Аппарат z-преобразования играет для
цифровых систем ту же роль, что и
преобразование Лапласа для непрерывных
систем.
Дискретное преобразование Лапласа
Введём
переменную
(T – период квантования, z – комплексная переменная) Изображения входной и выходной величин:
-преобразование
Дискретная передаточная функция:
|
Пример:
Весовая функция:
Заметим, что
|
Пример:
Решение: 1) представим приведённую непрерывную часть в виде суммы:
2) для получения весовой функции применим обратное дискретное преобразование Лапласа:
3) 4)
|
1)
чтобы по известной функции времени
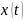 найти ее -изображение, необходимо лишь
каждое дискретное значение
найти ее -изображение, необходимо лишь
каждое дискретное значение
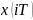 умножить на
умножить на
 ,
а затем свернуть получившийся степенной
ряд в конечную сумму;
,
а затем свернуть получившийся степенной
ряд в конечную сумму;
2)
чтобы по известному изображению
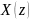 найти соответствующий сигнал
,
необходимо представить изображение
в виде степенного ряда по убывающим
степеням
,
получающиеся при этом числовые
коэффициенты ряда и есть дискретные
значения
сигнала
.
найти соответствующий сигнал
,
необходимо представить изображение
в виде степенного ряда по убывающим
степеням
,
получающиеся при этом числовые
коэффициенты ряда и есть дискретные
значения
сигнала
.
Для дискретных и дискретно-непрерывных
систем вводится понятие дискретной
передаточной функции. Пусть
![]() —
входной дискретный сигнал такой системы,
а
—
входной дискретный сигнал такой системы,
а
![]() —
её дискретный выходной сигнал,
—
её дискретный выходной сигнал,
![]() .
Тогда передаточная функция
.
Тогда передаточная функция
![]() такой системы записывается в виде:
такой системы записывается в виде:
![]() ,
где
,
где
![]() и
и
![]() —
z-преобразования для сигналов
и
соответственно:
—
z-преобразования для сигналов
и
соответственно:
![]() ,
,
![]() .
.
IV) Свойства z-преобразования:
• Линейность.
•
Свойство задержки (задержка исходного
сигнала на m отсчётов
добавляет множитель
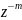 к
к
 -преобразованию
сигнала).
-преобразованию
сигнала).
• Теорема о свертке ( -преобразование свертки сигналов равно произведению их -образов).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дискретная передаточная функция:
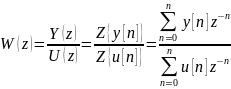
+-32. Импульсные системы. Формирователь импульсов (уравнение, передаточная функция, виды импульсной модуляции).
см. пункт 31
33. Уравнения импульсных систем в форме пространства состояний.
34. Цифровые системы. Структуры цифровых систем. Экстраполяторы в цифровых САУ. Передаточная функция экстраполятора нулевого порядка.
35. Z-преобразование и его свойства. Передаточные функции цифровых систем. Получение передаточной функции из разностного уравнения системы.
36. Частотные и временные характеристики цифровых и импульсных систем.
37. Устойчивость линейных импульсных и цифровых систем.
38. Определение нелинейной системы. Классификация, Особенности. Виды статических характеристик нелинейных элементов.
39. Задачи и методы исследования нелинейных систем. Исследование нелинейных систем в пространстве состояний.
40. Метод фазовой плоскости. Основные характеристики фазовых портретов нелинейных систем.
41. Режим автоколебаний в нелинейных системах.
42. Скользящие режимы в нелинейных системах. Системы с переменной структурой.
43. Метод точечного преобразования.
44. Метод припасовывания
45. Гармоническая линеаризация нелинейных элементов. Передаточная функция нелинейного элемента.
46. Метод гармонического баланса для однозначной нелинейности.
47. Метод гармонического баланса для неоднозначной нелинейности.
48. Устойчивость нелинейных систем по Ляпунову. Виды устойчивости. Прямой метод Ляпунова.
49. Критерий абсолютной устойчивости В.М. Попова.
50. Вероятностные характеристики случайных величин.
51. Понятие случайного процесса и его характеристики. Корреляционные функции непрерывных случайных процессов.
52. Спектральная плотность непрерывных случайных процессов. Понятие белого и «цветного» шумов.
53. Прохождение случайного сигнала через линейную систему.
54. Расчёт установившихся ошибок в линейной системе при случайных воздействиях. Расчёт линейной системы по минимуму среднеквадратической ошибки.


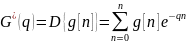
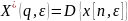
 ,
,
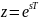
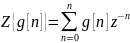

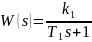

 ,
тогда получим
,
тогда получим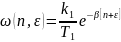 ,
где
,
где
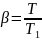
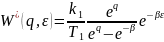
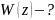

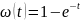 →
→