2. Сетевые методы планирования

Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ, заданного в специфической форме сети, графическое изображение которой называется сетевым графиком (графом). Главными элементами сетевой модели являются события и работы.

Термин работа используется в широком смысле:

1) действительная работа (возведение стен, окраска труб и т.д.);

2) ожидание (процесс сушки, отвердения бетона и т.д.);

3) зависимость или фиктивная работа - логическая связь между двумя или несколькими работами.

Работы видов 1) и 2) имеют известную положительную длительность. Работы вида 3) имеют нулевую длительность.

Событие - момент завершения какого-либо процесса, отдельного этапа выполнения проекта.

Событие может являться частным результатом отдельной работы или суммарным результатом нескольких работ. Среди событий сетевой модели выделяют исходное (начальное событие, которому не предшествуют другие события и работы) и завершающее (событие, которое не предшествует ни одному событию и не является началом ни одной работы).

События на сетевом графике (графе) изображаются кружочками (вершинами графа), а работы дугами. Сетевая модель должна удовлетворять следующим правилам:

1. В сетевой модели должно быть ровно одно исходное и ровно одно завершающее событие. 2. В сети не должно быть контуров. 3. Любые два события должны быть непосредственно связаны не более, чем одной работой.

Составим и исследуем сетевой график. Для исследования сетевого графика будем применять метод критического пути. Перейдем к составлению сетевого графика. Нам понадобится упорядочить вершины графа. Для упорядочения вершин применяется метод разбивки графа на слои.

Разбить все вершины ориентированного связного графа без контуров на слои означает, что множество вершин графа нужно разбить на подмножества S⁽¹⁾, S⁽²⁾,...,S^(k), называемые слоями, удовлетворяющие следующим условиям :

1) все элементы данного слоя S⁽ⁱ⁾ не имеют предков в следующих слоях S⁽ⁱ⁺¹⁾, S⁽ⁱ⁺²⁾,..., S^(k), элементы первого слоя не имеют предков, а элементы последнего потомков;

2) порядок вершин из одного слоя безразличен, т.е. не существует пути, соединяющего вершины одного слоя.

Разбиение на такие слои всегда существует.

Первый метод разбивки на слои. Составим матрицу смежности. Затем вычислим столбец V0, каждый элемент которого есть сумма по соответствующей строке элементов матрицы смежности. Вектор Vo содержит некоторое число нулей, это означает, что эти вершины не имеют потомков, они образуют слой 0. Далее вычислим столбец V1 , вычитая из столбца V0 столбец матрицы смежности, соответствующий вершине, вошедшей в нулевой слой. Те же операции проделываем для остальных слоев

Поиск критического пути. Вычислим ожидаемое время выполнения событий - (максимальное время). Расчеты осуществляются от слоя к слою. Теперь, двигаясь назад из завершающей вершины, находим дуги, на которых получилось время . Эти дуги составят критический путь или критические пути, если их несколько.

Любое замедление в выполнении критических работ или в наступлении критических событий приведет к соответствующему замедлению выполнения всего проекта. У событий и работ, не являющих­ся критическими, есть некоторый резерв.

Резервы времени событий.

Для каждого события i есть два граничных срока: время - ожидаемое время наступления события i; время - предельное время наступления события i.

Для критических событий имеет место равенство = , для некритических  .

Интервал [ , ] называется интервалом свободы, а его длина R(i) = - . называется резервом времени события i.

Резервы времени работ.

Полным резервом (i,j) работы (i,j) называется максимально возможная величина, на которую можно увеличить время выполнения данной работы при условии, что событие i наступило в ожи­даемое время , а срок выполнения всего проекта не изменится (i,j)= - - t(i,j) .

Пусть событие i наступило в ожидаемое время . Тогда свободным резервом R_c(i,j) работы (i,j) называется часть полного резерва, на которую можно увеличить продолжительность работы, не из­меняя при этом раннего срока ее конечного события j. R_c(i,j) = - - t(i,j) .

Независимым резервом R_н(i,j) работы (i,j) назы­вается величина, на которую возможна задержка работы (i,j) при условии, что начальное событие i наступает в предельно позднее время , а конеч­ное событие j в наиболее раннее время , т.е. R_н(i,j) = max{0; - - t(i,j)} .

Частным резервом R₁(i,j) работы (i,j) называется часть полного резерва, на которую можно увеличить продолжительность работы (i,j) при условии, что начальное и конечное события наступают в свои самые поздние сроки и . R₁(i,j)= - - t(i,j)

Определение максимальной пропускной способности сети

∙ 1 источник, 1 сток. Каждой дуге приписана пропускная способность. d_ij – пропускная способность дуги ij. x_ij – количество вещества, пропускаемого по дуге ij в единицу времени

0≤ x_ij ≤ d_ij

∙ Для любой вершины, кроме истока I и стока S, количество поступающего вещества в эту вершину, равно количеству вещества, вытекающего из нее. В промежуточных вершинах потоки не создаются и не исчезают.

∙ Общее количество вещества, вытекающего из истока I, совпадает с общим количеством вещества, поступающего в сток S

∙ Задача о максимальном потоке заключается в нахождении такого потока по транспортной сети, что сумма потоков из истока, или, что то же самое, сумма потоков в сток максимальна.

∙ Каждое неориентированное ребро (u, v) заменяем на пару ориентированных рёбер (u, v) и (v, u).

∙ Для произвольной сети максимальная величина потока из v_s в v_t равняется минимальной пропускной способности разреза, который отделяет v_s от v_t

∙ Алгоритм Форда — Фалкерсона

1. Обнуляем все потоки. Остаточная сеть изначально совпадает с исходной сетью.

2. В остаточной сети находим любой путь из источника в сток. Если такого пути нет, останавливаемся.

3. Пускаем через найденный путь (он называется увеличивающим путём или увеличивающей цепью) максимально возможный поток:

   1. На найденном пути в остаточной сети ищем ребро с минимальной пропускной способностью .

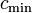   2. Для каждого ребра на найденном пути увеличиваем поток на , а в противоположном ему — уменьшаем на .

   3. Модифицируем остаточную сеть. Для всех рёбер на найденном пути, а также для противоположных им рёбер, вычисляем новую пропускную способность. Если она стала ненулевой, добавляем ребро к остаточной сети, а если обнулилась, стираем его.

4. Возвращаемся на шаг 2.

Алгоритм поиска кратчайшего пути при наличии дуг с отрицательной стоимостью – я у него спросила про этот пункт, он сказал, что, наверняка, уберет его)

G {E,V}, d_ij стоимость перехода из I в j

Найти путь из начальной вершины в конечную с минимальной суммарной стоимостью

N – множество непомеченных вершин

П – множество помеченных вершин

Шаг 0. ε₀ т.к. мы находимся в этой точке, то переход в нее =0

П=v₀

N={v₁:v_n}

Шаг 1.

Находим начальные дуги (I,j), такие что

V_i ∊ П, v_j ∊ N для каждой такой дуги определенное число N_ij = ε_i + d_ij

Шаг 2.

έ=min{h_ij}

Выделяем дуги, на которых этот минимум достигается. Конечную вершину помечаем ε_i =έ

Шаг 3.

Поверяем выполнение условия ε_i + d_ij≥ ε_d для всех дуг, вершины которого ∊П (V_i ∊ П, v_j ∊ П) - проверка на то, не существует ли более короткого пути, чем найденный

∙ если неравенство выполняется, то – Шаг 5

∙ если неравенство не выполняется, то – Шаг 4

Шаг 4.

ε_j* = ε_i + d_ij*

У дуги, на которой достигалась старая ε пометка отменяется, помечается новая дуга ij

Пусть

То есть появляется более короткий путь. Необходимо отменять пометку в мин (в нач.) и отметить дугу

Шаг 5.

Определяем помечена ли последняя вершина V_n ∊ П

Если v_n - конечная вершина помечена, то ответ

Если конечная вершина непомечена, то к Шаг 1

Кратчайший путь ищется из конечной вершины

Определение кратчайшего пути (2 пункта)

Задача о потоке минимальной стоимости

Расписаны в учебнике «Теория игр. Исследование операций» Костевича и Лапко

Динамическое программирование

ДП представляет собой математический аппарат, используемый для решения большого ряда задач математического программирования (на экстремум).

Характерным для ДП является разбиение исходной задачи на множество более мелких задач (этапы).

Заслуга создания и развития ДП принадлежит, прежде всего, Беллману.

ДП основано на принципе оптимальности. Оптимальное решение большой задачи может состоять только из оптимальных решений малых задач.

Принцип оптимальности:

Оптимальное поведение в многошаговом процессе обладает тем свойством, что каким бы ни было решение, принятое на последнем (текущем) шаге и состояние процесса перед очередным шагом, надо

выбрать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был оптимальным».

Три условия выполнения принципа оптимальности:

1. Частные подзадачи и исходная задача должны принадлежать одному классу сходных задач. Каждая подзадача характеризуется небольшим кол-вом переменных называющихся рамками состояния.

2. Предыстория системы не имеет значение для принятия будущих решений (принцип отсутствия последствий). Решение текущей задачи не имеет влияния на решения предыдущих задач.

3. Функция агрегирования, т.е. функция получения общего решения из решений частных задач является условием аддитивности (суммарности) целевой функции задачи