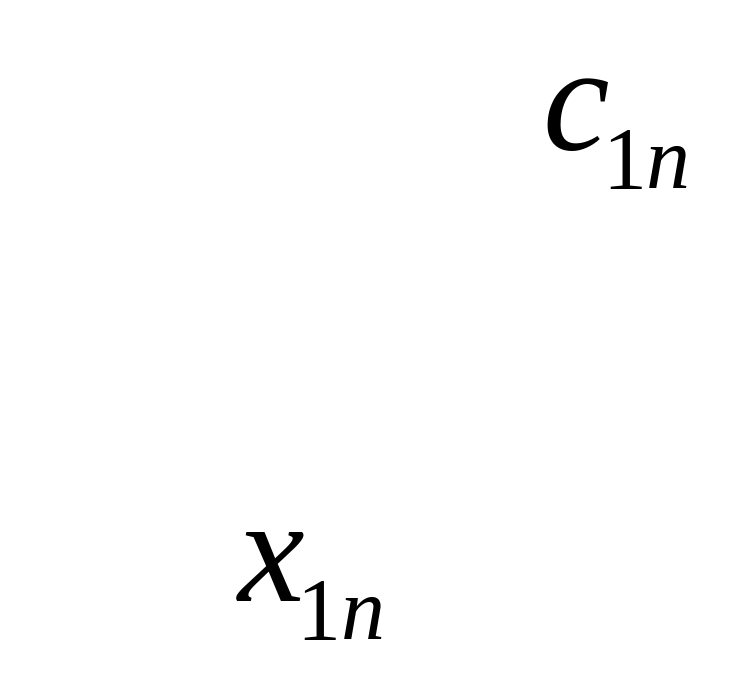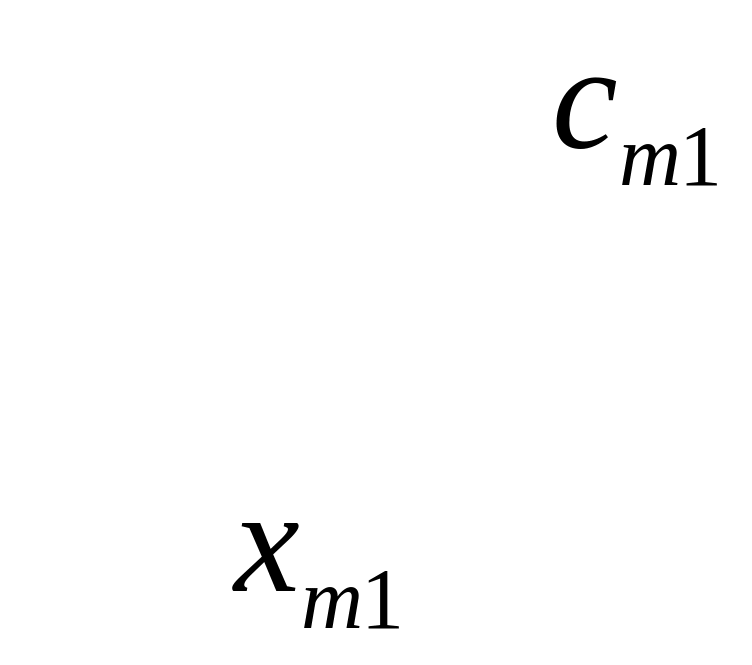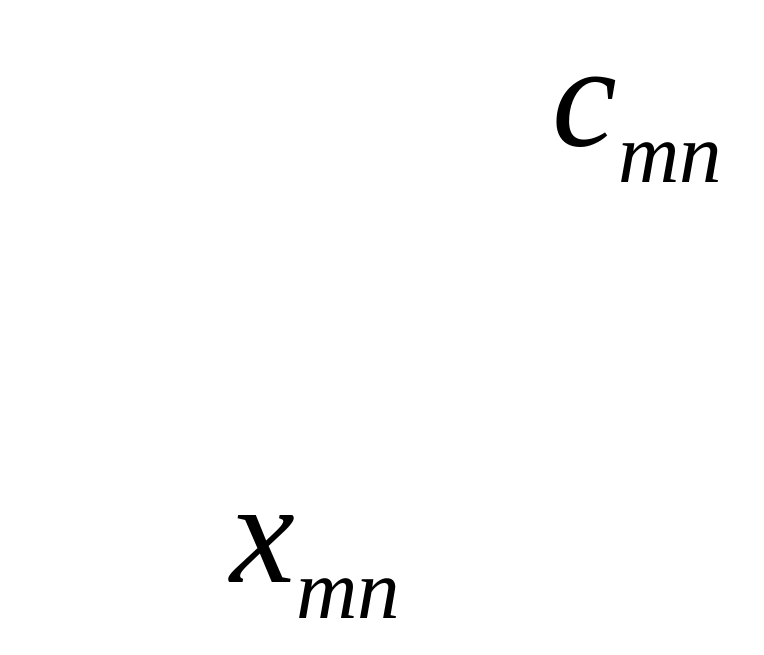Ценовой анализ

Нижний и верхний пределы изменения цены 1 определяются значениями коэффициента с, при которых наклон целевой прямой совпадает соответственно с наклонами прямых ограничений.

Изменение оптимального плана может быть связано с изменением цен на продукцию (коэффициентов при переменных в целевой функции). При небольших изменениях цен оптимальный план обычно сохраняет свою оптимальность. При существенных изменениях цен оптимальным становится другой план. Важно разобраться в этом, рассчитать критические ценовые границы.

Небольшое изменение этой цены приведет к незначительному повороту градиента (вместе со всей системой перпендикулярных ему линий уровня целевой функции). В результате оптимальный план останется в прежней точке. При более значительном изменении цены он перейдет в другую вершину области допустимых планов.

Верхняя критическая граница Критическая величина цены, при которой происходит переход оптимального плана из одной точки в другую, соответствует положению, когда линия уровня целевой функции параллельна прямой А₁А₂ (- линия ограничения в примере) (а градиент, соответственно, перпендикулярен этой прямой). Условием параллельности прямых является пропорциональность коэффициентов при переменных в двух уравнениях: линии уровня целевой функции и линия ограничения.

Нижняя критическая граница

Аналогичным образом рассчитывается нижняя граница цены первого продукта. При уменьшении цены первого продукта градиент вместе с линиями уровня будет поворачиваться против часовой стрелки. При достаточно сильном повороте оптимальный план перейдет в другую точку. Критическое положение определяется из условия параллельности линии уровня целевой функции и линии ограничения D1D2.

Транспортная задача

1. Математическая постановка задачи. Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления A₁, A₂,…, A_m в n пунктов назначения B₁,B₂,…,B_n. При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок груза.

Обозначения:

1,……, m- поставщики груза, - запас этого груза на складе,

1, …..n-потребителей, - размер потребления груза, - стоимость перевозки 1 единицы груза от -го поставщика к -му потребителю.

строка (i)-поставщики

столбец(j)-потребитель

Составим план перевозок от поставщиков к потребителям, при котором у поставщиков будет вывезен весь груз, а потребителям будет завезено столько, сколько им нужно, при этом суммарная стоимость перевозок должна быть минимальной.

Вводим переменные - количество единиц груза, перевозимого от i-ого поставщика к -му потребителю, ,

F = , где с_ij – матрицей стоимостей перевозок

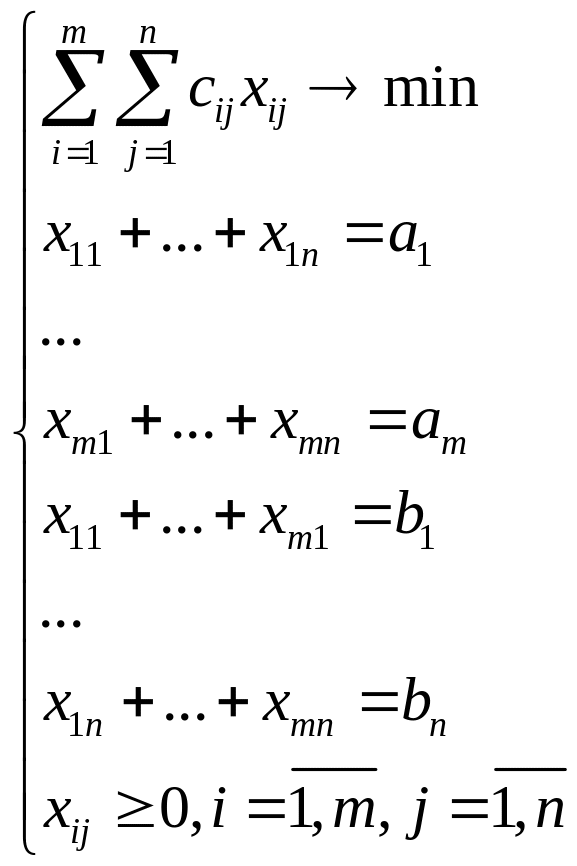
Опр1. Матрица X с неотрицательными элементами x_ij называется планом перевозок.

Опр2 План X^*=(х_ij^*), i=1,…, m, j=1,….,n, при котором функция принимает свое минимальное значение, называется оптимальным планом транспортной задачи.

Исходные данные транспортной задачи записываются в виде таблицы:

Пункт отправления	Пункт назначения				Запасы
	B1	…	…	Bn
A1					a1
…	…	…	…	…	…
…	…	…	…	…	…
Am					am
	b1	…	…	bn

- общее наличие груза у поставщиков, - общая потребность в грузе

Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, то есть

то модель такой транспортной задачи называется закрытой. Если же указанное условие не выполняется, то модель – открытая.

Теорема: Для разрешимости транспортной задачи необходимо и достаточно, чтобы выполнялось равенство:

Чтобы решить открытую задачу сведем ее к предыдущей.

1)Если a>b, вводим фиктивного потребителя c потребностью: .

Стоимость перевозки этому потребителю .

Все что получает фиктивный потребитель останется на складе у поставщика.

2)Если a<b, то вводим фиктивного поставщика , с_m+1j=0, j=

Все что фиктивный поставщик поставит, соответствующий потребитель не дополучит.

Условие закрытости транспортной задачи a = b означает, что среди m + n уравнений системы независимыми являются только m + n – 1 уравнений, поэтому в любом базисном решении этой системы должно быть m + n - 1 базисных переменных. Поскольку свободные переменные в таком

решении равны нулю, то в транспортной таблице им будут соответствовать пустые клетки.

· Клетки таблицы, в которые записаны отличные от нуля перевозки,

называются занятыми, а остальные (пустые) - свободными.

· План называется вырожденным, если количество занятых клеток в нем меньше, чем n + m -1.

План называется невырожденным, если количество занятых клеток равно в точности n + m – 1

Если на каком-то этапе решения получился вырожденный план, то его необходимо пополнить, проставив в недостающем числе клеток нулевую перевозку и превратив, тем самым, эти клетки в занятые.

· Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией так, чтобы две соседние вершины ломаной были расположены либо в одной строке, либо в одном столбце. План называется ациклическим, если его занятые клетки не содержат циклов. В опорном плане не может быть циклов. Оптимальные планы являются ациклическими, поэтому и первоначальный план также должен удовлетворять этому требованию. Планы, полученные с помощью метода северо-западного угла и метода наименьшей стоимости, ациклические.

Схема решения:

1)найти начальный опорный план.

2)проверить план на оптимальность.

3)если план не оптимальный, то перейти к новому опорному плану (результат не хуже предыдущего).

Методы для определения опорного плана:

1. Метод северо-западного угла

2.Метод минимального элемента

(3. Метод Фогеля)-можно видимо не писать раз про него нам не рассказывали