3 . Основное неравенство двойственности

C₁X₁+… +C_NX_N→ max b₁y₁+…+ b_my_m→ min

a₁x₁+… +a_1nx_n<=b₁ :У₁ a_ny₁ + a₂₁y₂+…+a_m1y_m>=c₁

(1) a_m1x₁+…+a_mnx_n<=b_1т :у_ь (2) a_1m1y₁ + …+a_mn1y_m>=c_n

x_j>=0, j=1,n; y_i>=0, i=1,m

Для любых допустимых планов прямой и двойственной задачи ЛП справедливо неравенство:

Доказательство: из дв.задачи (2)

Для любого допустимого плана пр-ва Х и любого доп-го вектора оценок У (с₁х₁+…+ с_nх_n) общая стоимость произведенной продукции не превосходит суммарной оценки рес-сов (b₁y₁+…+ b_my_m) .

4. Теоремы двойственности

1. Критерий оптимальности Канторовича.Если для некоторых допустимых планов х* и у* пары двойственных задач (1)и(2) выполняется равенство f(x)=g(y): C₁X₁+… +C_NX_N= b₁y₁+…+ b_my_m, то х* и у* являются оптимальными планами соответствующих задач.Док-во. Согласно основному неравенству двойственности, для любого допустимого плана х* прямой задачи и допустимого плана у двойственной справедливо неравенство g(y) < f(x*). Но по условию g(y*) = f(x*). Отсюда в силу транзитности отношений < и =, получим g(y)< g(y*). Так как у – произвольный план, то g(y*) есть максимальное значение целевой функции, то есть у – оптимальный план двойственной задачи. Аналогично доказывается, что х* является оптимальным для прямой задачи.

2.Основная теорема дв-ти:Если одна из задач двойственной пары имеет оптимальное решение, то и другая имеет оптимальное решение. Если же 1 из дв-ных задач не имеет решений на мн-ве доп.планов вследствии неограниченности целевой функции, то и 2 не имеет решения в силу пустоты мн-ва доп.планов. Т.е. если прямая задача имеет опт.решение, то дв-ная к ней также имеет опт.решение. Причем значение цел.функции на опт.планах прямой и дв-ной задач совпадают: F(X^*)=G(Y^*)

Экономическое содержание первой теоремы двойственности состоит в следующем: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученной при реализации оптимального плана, совпадает с суммарной оценкой ресурсов.

3.Теорема о дополняющей нежесткости:

Для того чтобы X^*=( X₁^*, .. X_n^*) и У^*=( У₁^*, .. У_n^*) являлись оптим. планами прямой и двойственной задач, необх-мо и дост-но, чтобы выполнялись след.соотношения:

               Экономически это означает, что если по некоторому оптимальному планупроизводства расход i -го ресурса строго меньше его запаса, то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равна нулю. Если же в некотором оптимальном плане оценок его i -я компонента строго больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен его запасу. Отсюда следует вывод: двойственные оценки могут служить мерой дефицитности ресурсов. Дефицитный ресурс (полностью используемый по оптимальному плану производства) имеет положительную оценку, а ресурс избыточный (используемый не полностью) имеет нулевую оценку.

4.Теорема об оценках:

F(x) – значение целевой функции в оптимальном плане

-значение целевой функции зависит от вектора b

Двойственные оценки переменных показывают приращение целевой функции , вызванное изменением свободного члена соответствующего ограничения:

Значения переменных y_i в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов b_i системы ограничений – неравенств прямой задачи на величину

 После того как оптимальное решение получено, может быть выявлена чувствительность к определенным изменениям исходной модели. В связи с этим возможно установить следующее.

-Увеличение какого из ресурсов наиболее выгодно (ценность ресурсов).

-На сколько можно увеличить запас сырья для улучшения полученного значения целевой функции (чувствительность решения к изменению запасов сырья).

-Каков диапазон изменения того или иного изменения коэффициента целевой функции, при котором не происходит изменения оптимального решения (чувствительность решения к изменению коэффициентов целевой функции).

-Целесообразность включения в план новых изделий.

 Замечание: если F(x) невырожденная , то существует относительность точки и (b), такая, что

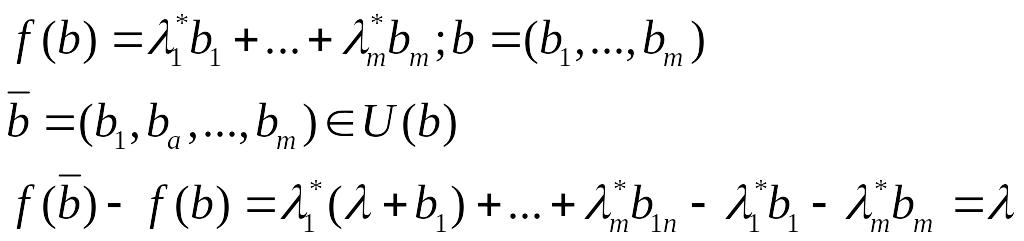
Показывает, на сколько увеличиться целевая функция, если соответствующий ресурс увеличить на 1.

Анализ на чувствительность

На практике многие экономические параметры (цены на продукцию и сырье, запасы сырья, спрос на рынке, заработная плата и т.д.) с течением времени меняют свои значения. Поэтому оптимальное решение задачи ЛП, полученное для конкретной экономической ситуации, после ее изменения может оказаться непригодным или неоптимальным. В связи с этим возникает задача анализа чувствительности задачи ЛП, а именно того, как возможные изменения параметров исходной модели повлияют на полученное ранее оптимальное решение.

Выделяют следующие три задачи анализа на чувствительность:

1. Анализ сокращения или увеличения ресурсов: а) на сколько можно увеличить или уменьшить запас дефицитного ресурса для улучшения оптимального значения ЦФ? б) на сколько можно уменьшить или увеличить запас недефицитного ресурса при сохранении полученного оптимального значения ЦФ? 2. Увеличение (уменьшение) запаса какого из ресурсов наиболее выгодно? 3. Анализ изменения целевых коэффициентов: каков диапазон изменения коэффициентов ЦФ, при котором не меняется оптимальное решение? - имеется в виду диапазон цен

Можно сформулировать правила получения двойственной задачи из задачи исходной:

1. Если в исходной задаче ищется максимум целевой функции, то в двойственной ей - минимум.

2. Коэффициенты при переменных в целевой функции двойственной задачи являются свободными членами системы ограничений исходной задачи.

3. В исходной ЗЛП все функциональные ограничения - неравенства вида “≤”, а в задаче, двойственной ей, - неравенства вида “≥”.

4. Коэффициенты при переменных в системах ограничений взаимно двойственных задач описываются матрицами, транспонированными относительно друг друга.

5. Число ограничений в исходной задаче совпадает с числом переменных в двойственной.

6. Условие неотрицательности переменных сохраняется в обеих задачах.

Свойства двойственных оценок:

Свойство 1. Оценки как мера дефицитности ресурсов. Двойственные оценки отражают сравнительную дефицитность факторов производства (дефицитный ресурс - полностью используемый по оптимальному плану производства). Чем выше величина оценки , тем выше дефицитность i-го ресурса. Факторы, получившие нулевые оценки, не являются дефицитными и не ограничивают производство.

Свойство 2. Оценки как мера влияния ограничений на значение целевой функции. Величина двойственной оценки какого-либо ресурса показывает, насколько возросло бы максимальное значение целевой функции, если бы объем данного ресурса увеличился на единицу. В связи с этим значение объективно обусловленной оценки иногда называют теневой ценой ресурса. Теневая цена - это стоимость единицы ресурса в оптимальном решении.

Однако нужно учитывать, что двойственные оценки позволяют измерить эффективность лишь незначительного изменения объема ресурсов. При значительных изменениях может быть получен новый оптимальный план и новые двойственные оценки.

Такого не было, если я не ошибаюсь) Свойство 3. Оценки как инструмент определения эффективности отдельных хозяйственных решений. С помощью двойственных оценок можно определить выгодность выпуска новых изделий, эффективность новых технологических способов производства. При этом эффективным может считаться тот вариант производства, для которого сумма прибыли, недополученной из-за отвлечения дефицитных ресурсов, будет меньше прибыли получаемой. Разница между этими величинами (Δ_j) вычисляется как:

(2.9)

В том случае, если Δ_j ≤ 0, вариант производства является выгодным, если Δ_j > 0 – вариант невыгоден.

И такого) Свойство 4. Оценки как мера относительной заменяемости ресурсов с точки зрения конечного эффекта. Например, отношение / показывает, сколько единиц k-го ресурса может быть высвобождено при увеличении объема i-го ресурса на единицу, для того чтобы максимум целевой функции остался на прежнем уровне; или наоборот, сколько единиц k-го ресурса необходимо дополнительно ввести при уменьшении на единицу объема i-го ресурса, если мы хотим, чтобы значение целевой функции не изменилось.