Элементы математической статистики Основные понятия математической статистики

Пусть имеется множество однородных объектов с различными количественными параметрами. Надо объекты распределить на группы с одинаковыми параметрами и определить их число по каждой группе. Если сплошное обследование невозможно, то исследуют часть объектов. Тогда множество всех объектов наз. генеральной совокупностью, а случайно отобранные объекты наз. выборкой. Пр. Партия деталей с некоторым разбросом размеров.

Задача математической статистики – зная некоторые свойства подмножества элементов, сделать выводы о свойствах всего множества.

Полное число объектов генеральной совокупности N наз. её объемом. Параметры объектов образуют множество чисел А (аргументов) с некоторым распределением. Извлечение объекта есть испытание, результат которого СВ Х, а х – её реализация. Ожидаемое значение СВ M(X) и её дисперсия D(X) являются характеристиками распределения генеральной совокупности. Случайная выборка n объектов приводит к СВ X₁, X₂, . . . , X_n, для которых M(X_i) = M(X), D(X_i) = D(X). Поэтому исследование выборки дает оценку распределения генеральной совокупности.

Опр. Генеральной средней (или а) наз. среднее арифметическое значений параметров генеральной совокупности

= = ( 1 )

где N_i – частота повторения х_i , K – число различающихся значений х*_i (вариант). Они образуют множество X*. Отношение частоты N_i к объему выборки есть вероятность появления варианты х*_i при случайной отборе объекта: p_i = _. Поэтому ( 1 ) определяет также и МО СВ Х генеральной совокупности: M(X) = . Кроме того, =N или

Составим таблицу результатов выборки n элементов

I	1	2	3		N
X	x1	x2	x3	. . .	xn

объединим равные значения СВ

X*	x*1	x*2	x*3	. . .	x*l
nx	n1	n2	n3	. . .	nl

где n_i - наз. частотой появления значения х_i . Сумма всех частот равна объему выборки . Относительной частотой наз. отношение частоты n_i к объему выборки p*_i = n_i / n. Таблица соответствия вариант х*_i и относительных частот p*_i наз. статистическим рядом.

( 2 )

X*	x*1	x*2	x*3	. . .	x*l
P*	p*1	p*2	p*3	. . .	p*l

Генеральную совокупность определяет аналогичный статистический ряд, куда входят все возможные варианты и вместо относительных частот p*_i стоят вероятности p_i.

Если Х - непрерывная СВ на большом интервале (a,b), то его разбивают на l малых интервалов (a_i , a_i+1) с шагом h = a_i+1 - a_i , определяют относительную частоту попадания в каждый из них и получают статистический ряд по интервалам.

( 3 )

X*		(a,a1)		(a1,a2)	(a2,a3)		. . .		(al-1,b)
P*	p*1		p*2		p*3	. . .		p*l

Если испытания приводят к пограничной точке a_i c частотой n_i , то n_i распределяют поровну между соседними интервалами.

Статистический ряд дискретных СВ иллюстрирует полигон. Это ломаная линия в системе координат хОр , соединяющая соседние точки (х*_i , p*_i ) .

С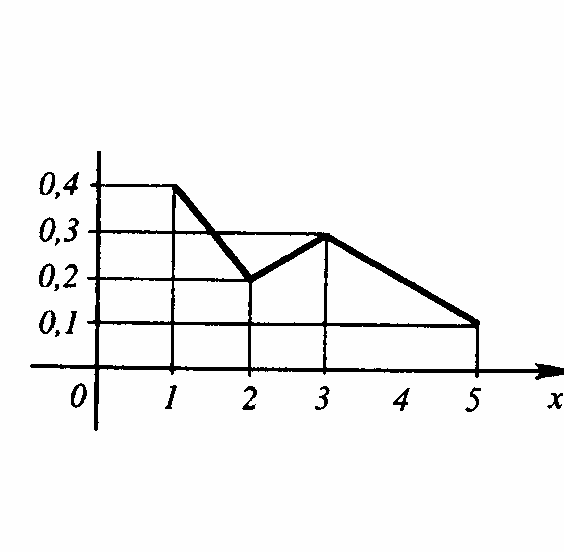 татистический ряд непрерывных СВ иллюстрирует гистограмма. В системе координат хОр из точек а_i восстанавливают перпендикуляры и над каждым интервалом (a_i,a_i+1) на высоте p*_i / h , где h - шаг таблицы, проводим линию | | Ox . Получается ступенчатая фигура, где площадь каждого прямоугольника равна p*_i , а площадь всей фигуры 1.

С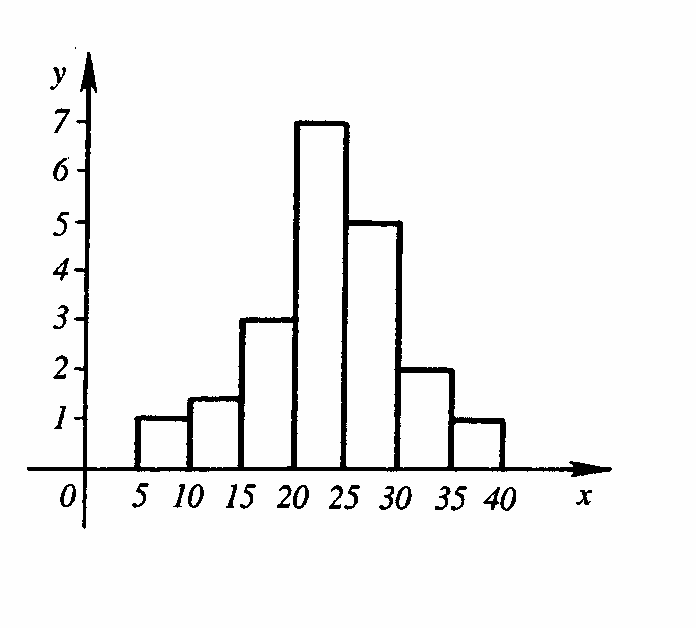 умма площадей первых k прямоугольников гистограммы определяет относительную частоту появления СВ Х в области Х < x_k , а движение вдоль всей гистограммы дает эмпирическую функцию распределения.

F_n*(x) = 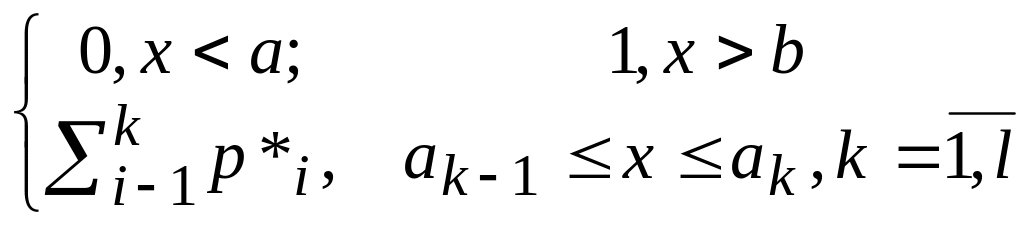( 4 )

Опр. Выборочной средней наз. среднее арифметическое значений параметров статистического ряда ( 2 )

= ( 5 )

Если выборки объема n из A повторять много раз, то получим разные значения . Это реализации случайной величины =1/n ( X₁+ X₂ +. . . + X_n).

МО средней СВ совпадает с МО СВ Х и генеральной средней:

M( ) = = M(X) .

M( ) = M[1/n ( X₁ + X₂ +. . .+ X_n)] = (1/n)[M(X₁) + M(X₂) +. . .+ M(X_n)] = (1/n)[M(X) + M(X) +. . .+ M(X)] = M(X) = .

Вычислим дисперсию от выборочной средней СВ

D( ) = D( ) = = = ( 6 )

т.к. D(X+Y) = D(X) + D(Y); D(CX) = C² D(X); D(x_i) = D(X).

Опр. Генеральной дисперсией D_Г наз. среднее арифметическое квадратов отклонения параметров генеральной совокупности от генеральной средней D_Г = = ( 7 )

а генеральным средним квадратичным отклонением наз. .

Дисперсия СВ Х совпадает с генеральной дисперсией: D(X) = D_Г .

D(X) = M{[X – M(Х)]²} = = D_Г, т.к. M(X) = , а

P{X= x_i} = 1/N. Формула ( 6 ) теперь примет вид D( ) = .

Опр. Выборочной дисперсией D_В наз. среднее арифметическое квадратов отклонения параметров выборочной совокупности от выборочной средней D_В = = ( 8 )

а выборочным средним квадратичным отклонением наз. .

Если выборки объема n из A повторять много раз, то получим разные значения D_В. Это реализации случайной величины = .

Теорема. Математическое ожидание выборочной дисперсии равно

М( ) = ( 9 )