Нормальное распределение (распределение Гаусса)

Если изменение плотности вероятности f(x) около точки х будет пропорционально значению самой функции f(x) , приращению аргумента х , а также значению аргумента х , т.е f(x) = -  f(x) х х , то вид f(x) определяет дифференциальное уравнение , решение которого f(x) = С наз. кривой Гаусса. Эта функция имеет куполообразную форму, симметрична относительно оси Оу, быстро затухает. Замена х на (х – m) перемещает купол вдоль оси Ох.

З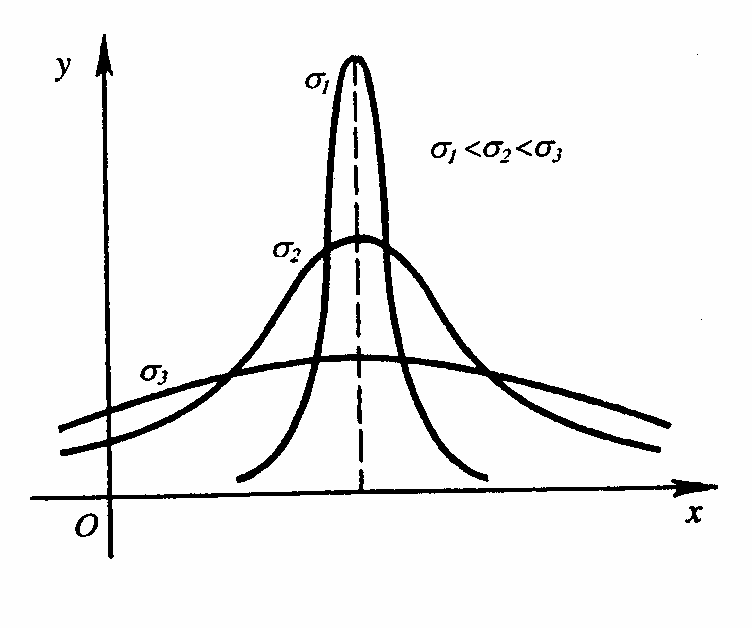 акон распределения вероятностей непрерывной случайной величины Х наз. нормальным, если её дифференциальная функция f(x) определяется формулой

f(x) = ( 32 )

где m – определяет точку максимума, т.е. ось симметрии и математическое ожидание M(X) = m.

 - расстояние от этой оси до точки перегиба, причем, D(X) = . Это распределение играет

фундаментальную роль в теории ошибок измерений. Согласно центральной предельной теореме закон распределения суммы большого числа независимых СВ, влияние каждого из которых на всю сумму ничтожно мало, близок к нормальному. Доказана А.М.Ляпуновым (1857 – 1918) .

Вероятности нормального распределения N(x; m,  ) :

P(a< X < b) = F(b) - F(a) = f(x) dx = dx ( 33 )

В случае m = 0,  = 1 функция ( 32 ) наз. плотностью нормированного и

центрированного распределения ( 34 )

а соответствующая функция распределения (х) = ( 35 )

наз. функцией Лапласа или интегралом вероятностей. (x) - нечетная функция и вычисляется с помощью таблиц. После простой замены переменных в ( 33 ) имеем

P(a<X<b) = [ –  ] ( 36 )

Вероятность отклонения Х от m на величину меньшую  по симметричному участку относительно m равна

P(|X – m| < ) = P(m -  < X < m + ) =  –  = 2 ( 37 )

Пр. 11. Определить среднее квадратичное отклонение  случайных ошибок прибора, если они подчиняются нормальному закону. Систематических ошибок прибор не имеет (m = 0), а случайные с вероятностью 0,8 не выходят за пределы 20 (м).

Решение. По условию задачи Р( |x| 20 ) = 0,8 или по формуле ( 37 )

 –  = 2 = 0,8. По таблице находим 20/ =1,29 или  = 15,5

Пр. 12. СВ Х распределена по нормальному закону с математиче6ским ожиданием m = 40 и дисперсией D = 1600. Вычислить вероятность попадания СВ в интервал (30, 80)

Решение. В формуле ( 36 ) a = 30, b = 80, m = 40,  =

P(30<X<80) =  –  = (1) + (0,25) = 0,34 + 0,1 = 0,35

Таблица значений функции Ф(х)

x	Ф(х)	x	Ф(х)	x	Ф(х)	x	Ф(х)	x	Ф(х)
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7	0 0,04 0,08 0,12 0,16 0,20 0,22 0,26	0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5	0,29 0,31 0,34 0,36 0,39 0,40 0,42 0,43	1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3	0,44 0,45 0,46 0,47 0,477 0,482 0,486 0,489	2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,2	0,491 0,493 0,495 0,496 0,497 0,498 0,498 0,499	3,4 3,6 3,8 4,0 4,5 5,0	0,499 0,499 0,499 0,499 0,499 0,500